시작하기 전에
π(파이)의 정의부터
학생들에게 파이가 뭐냐고 물으면
대부분 원주율이라고 대답합니다.
그럼 원주율은 뭔데요..?
파이요... ㅋ~
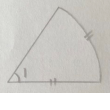
부채꼴의
반지름과 호의 길이가 같을 때의 각을
단위없이 1이라고 쓰고
1라디안이라고 읽습니다.
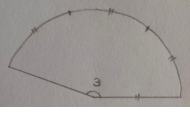
그럼, 호의 길이가 반지름의 길이의 2배면
그 때의 각은 당연히 2라디안

호의 길이가 반지름의 길이의 3배면
그 때의 각은 3라디안
그래서
이런 당연한 공식이 있죠
(호의 길이) = (반지름의 길이) x (중심각의 크기)
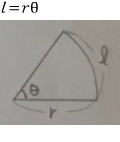
물론
이 때의 중심각은 라디안이어야 합니다.
어디서 한번쯤 본 공식이죠..?! ;;;;;
사실 공식이랄 거도 없이
반지름의 길이가 3이고, 중심각의 크기가 2라디안이면
호의 길이는 당연히 6 아닌가요..?!
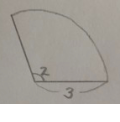
본론으로 돌아와서
그럼, 반원일 때
호의 길이는 반지름의 길이의 몇 배일까요..?

실제로 재어보니 딱 떨어지진 않지만
약 3.14배라는 걸 알게 됩니다.
앗..!! 그 3.14..?!
맞습니다. 그 3.14입니다.
우리가 원주율이라고 부르는
원의 크기와 관계없이 모든 반원의 호의 길이는
자기 반지름의 길이의 약 3.14배입니다.

그리고
이 때의 중심각을 3.1415... 라고 쓰면 좀 그러니까
간단하게 π라고 적습니다.
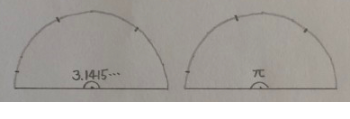
그래서
π=180˚라는 것이 등장하는 것입니다..!!
한가지 더 이야기하면
180˚를 3.14로 나눠보면 약 57˚입니다.
즉, 1라디안은 57˚정도 됩니다. 그렇기 때문에
sin1과 sin1˚는 천지차이입니다.
sin1≒sin57˚ 이니까요
여기서 하고 싶은 말은
중심각을 쓸 때는 정확히 구분하라는 것입니다.
라디안이면 라디안
도면 도
싸인 30도를 쓰면서
도(˚)를 안 쓰면
싸인 30도가 아니라
sin30≒sin(30x57˚)=sin1710˚ 가 돼 버립니다..!!
이제
라디안에 좀 익숙해져 볼까요
π=180˚ 에서 출발하면

90˚를 반으로 나누면 45˚
한칸씩 갈 때마다 45˚씩 증가합니다.

90˚를 세등분하면 30˚
한칸씩 갈 때마다 30˚씩 증가합니다.

두 칸씩 가면 60˚씩 증가합니다.

원으로 보면
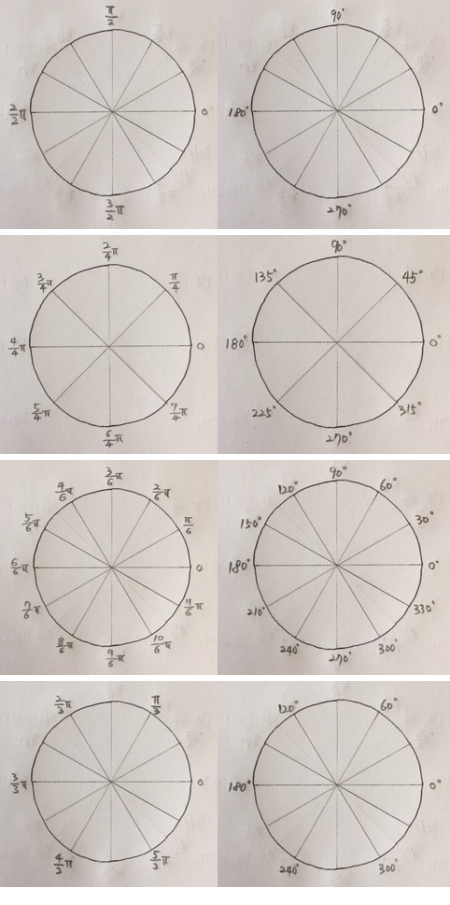
처음에는 좀 헷갈려도
문제 풀면서 계속 보다보면
금방(?) 익숙해질 거예요~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 삼각함수의 값 구하기 (1) (0) | 2021.10.24 |
|---|---|
| 삼각함수 그래프 (1) (0) | 2021.10.17 |
| 삼각비 (4) (0) | 2021.10.03 |
| 삼각비 (3) (0) | 2021.09.26 |
| 삼각비 (2) (0) | 2021.09.19 |