문제1)

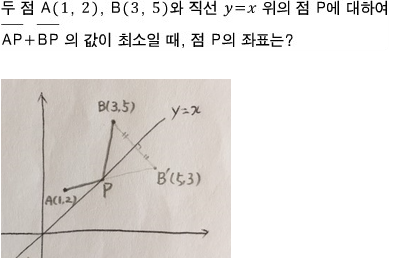
점 P를 아무데나 찍지말고
y=x 위에만 찍으라네요
그럼 y=x 위 어디에다 찍으면

위의 그림과 같이
점 B를 y=x 에 대칭시켰을 때
선분 AB'의 길이가

따라서

물론 점 A를 대칭시켜도
결과는 같습니다.

문제2)
두 점 A(1, 2), B'(5, 3)을 지나는 직선의 방정식을 구해서
y=x 와의 교점의 좌표를 구하겠습니다.
두 점 A, B'를 지나는 직선의 방정식은

y=x 와 연립해서 풀면

따라서, 점 P의 좌표는

확인 겸
아래 그림으로도 구해보면

두 점 A', B를 지나는 직선의 방정식은

y=x 와 연립해서 풀면

결과는 같습니다.
문제3)

우리가 문제1과 문제2에서
그림을 이용해서 문제를 푼 건
식으로 해결이 안되기 때문입니다.
P(a, a)로 놓으면

이 식의 최솟값을 구하라구요? ㅠ
음... 포기하고
그림을 이용해서 문제를 푼 것입니다.
근데, 이 문제는
식으로 바로 해결이 됩니다..!!

따라서

문제4)

문제5)
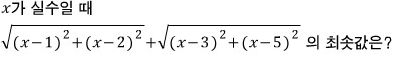
어라?
위에서 이 식의 최솟값은 못구한다고 해놓고
최솟값을 구하라구..?!
사실 산전수전 다 겪은 학생들은
다시 말해, 문제를 많이 풀어 본 학생들은
이 식을 해석해 냅니다. 이 어려운 걸..!!
우리도 한번 해석해 보죠.

이 식을 말로 해보면
(x, x), (1, 2) 사이의 거리와
(x, x), (3, 5) 사이의 거리의 합..!!
따라서, 이 문제는
(x, x), (1, 2) 사이의 거리와
(x, x), (3, 5) 사이의 거리의 합..!!의 최솟값을 구하라는 것이고
문제1

과 같은 문제라는 거..!! ;;;;;
문제6)

이 때는 두 점 A, B가 처음부터
y=x 를 기준으로 반대쪽에 있기 때문에

괜히 전에 풀어봤던 문제랍시고
문제파악도 안하고
점 B를 y=x 에 대칭시켜
(1, 2)와 (3, 5) 사이의 거리를 구한다거나

점 A를 y=x 에 대칭시켜
(2, 1)과 (5, 3) 사이의 거리를 구하면

안돼요~
문제7)

이 식을 말로 해보면
(x, x), (1, 2) 사이의 거리와
(x, x), (5, 3) 사이의 거리의 합..!!
따라서, 이 문제는
(x, x), (1, 2) 사이의 거리와
(x, x), (5, 3) 사이의 거리의 합..!!의 최솟값을 구하라는 것이고
문제6

과 같은 문제라는 거..!! ;;;;;
느꼈는지 모르겠지만
문제를 만드는 사람이 여러분을 낚으려고 마음 먹으면 한도 끝도 없습니다.
우리가 할 수 있는 거라고는
그저 문제를 잘 읽고 잘 파악하는 수 밖에 없다는 거... ㅠ
아직 안 끝났습니다. ;;;;;
두 점 (1, 2), (3, 5)가
y=x 를 기준으로
같은쪽에 있는지 반대쪽에 있는지
어떻게 확인하죠?
물론 좌표평면에
그림을 정확하게 그려서 확인해도 되지만
그림말고 식으로..!!
먼저 식을 한쪽으로 넘기고
x-y=0
x-y=0 에
(1, 2)를 대입하면 음수 (1-2=-1)
(3, 5)를 대입해도 음수 (3-5=-2)
양수냐, 음수냐는 관심없고
부호가 같냐, 다르냐를 확인합니다.
부호가 같으므로
두 점 (1, 2), (3, 5)는
y=x 를 기준으로 같은쪽에 있다는 거..!!
식을 반대쪽으로 넘겨볼까요
y-x=0
y-x 에
(1, 2)를 대입하면 양수 (2-1=1)
(3, 5)를 대입해도 양수 (5-3=2)
역시 부호가 같으므로
두 점 (1, 2), (3, 5)는
y=x 를 기준으로 같은쪽에 있습니다.
이번에는
(1, 2)와 (5, 3)을
한번 확인해 보겠습니다.
x-y 에
(1, 2)를 대입하면 음수 (1-2=-1)
(5, 3)을 대입하면 양수 (5-3=2)
부호가 다릅니다.
y-x 에
(1, 2)를 대입하면 양수 (2-1=1)
(5, 3)을 대입하면 음수 (3-5=-2)
역시 부호가 다릅니다.
따라서, 두 점 (1, 2), (5, 3)은
y=x 를 기준으로 반대쪽에 있습니다.
정리하면
기준이 되는 식을 한쪽으로 넘기고
좌표를 대입해서 부호가 같은지 다른지 확인..!!
부호가 같으면 같은쪽
부호가 다르면 반대쪽
양수인지 음수인지는 상관없어요~
다시 문제로 돌아와서

이런 문제를 맞닥들이면
제일 먼저
(1, 2)와 (5, 3)이
y=x 를 기준으로
같은쪽에 있는지
반대쪽에 있는지부터 확인해야 된다는 거..!!
그래야 그나마 좀 덜 낚입니다.
잊지 마세요~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 일차방정식의 해 (0) | 2020.11.24 |
|---|---|
| 두 점 사이의 거리 (5) (0) | 2020.11.20 |
| 두 점 사이의 거리 (3) (0) | 2020.11.16 |
| 두 점 사이의 거리 (2) (0) | 2020.11.06 |
| 두 점 사이의 거리 (1) (0) | 2020.11.05 |