소금물의 농도

이 글에 대한 AI '클로드'의 평가

 

(상세한 평가는 이 글 마지막에 있습니다.)

 

 

 

$농도=\frac{소금}{소금물}\times100=\frac{소금}{물+소금}\times100$

 

위의 공식만으로도 충분(?)하지만

굳이 하나 더 외우고 싶으면

 

$농도=\frac{소금}{소금물}\times100\quad\rightarrow\quad소금=\frac{농도}{100}\times소금물$

 

 

 

문제1)

물 200g에 소금 40g을 녹이면 농도는?

 

$\frac{40}{200+40}\times100≒16.7\%$

 

 

 

문제2)

20%의 소금물 300g에 녹아있는 소금의 양은?

 

$\frac{a}{300}\times100=20\quad\rightarrow\quad a=60$

 

소금의 양을 구하는 공식을 외웠으면

 

$\frac{20}{100}\times300=60$

 

 

 

문제3)

30%의 소금물 200g에 소금 10g을 더 녹이면 농도는?

 

처음에 들어있던 소금의 양은

 

$\frac{30}{100}\times200=60$

 

여기에 소금 10g을 더 넣었으니

 

소금은 70g이 되고

소금물은 210g이 됩니다.

 

따라서, 농도는

 

$\frac{70}{210}\times100≒33.3\%$

 

 

 

문제4)

30%의 소금물 200g에 물 10g을 더 부으면 농도는?

 

처음에 들어있던 소금의 양은

 

$\frac{30}{100}\times200=60$

 

여기에 물 10g을 더 부었으니

 

소금의 양은 변함이 없고

소금물만 210g이 됩니다.

 

$\frac{60}{210}\times100≒28.6\%$

 

 

 

문제5)

30%의 소금물 200g이 들어있는 그릇에서 50g의 소금물을 퍼내면

남아있는 소금의 양은?

 

처음에 들어있던 소금의 양은

 

$\frac{30}{100}\times200=60$

 

200g에 60g이 녹아있으니까

50g에는

 

$200:60=50:a\quad\rightarrow\quad a=15$

 

(소금이 균질하게(골고루) 녹아있다고 보는 것이 합리적이겠죠..?!)

 

그래서, 남아있는 소금의 양은

 

$60-15=45g$

 

 

 

눈치챘는지 모르겠지만

소금물의 농도 문제는 대부분 '소금의 양'을 가지고 문제에 접근합니다.

 

암튼 이 정도 했으면

소금물의 농도에 대한 기본적인 개념은 잡힌 걸로... ;;

 

 

 

문제6)

20%의 소금물 300g과 10%의 소금물 150g을 섞으면 농도는?

 

20%의 소금물 300g에는 소금이

 

$\frac{20}{100}\times300=60$

 

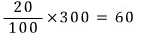
10%의 소금물 150g에는 소금이

 

$\frac{10}{100}\times150=15$

 

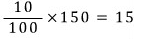
섞으면

 

소금은 60+15 = 75g

소금물은 300+150 = 450g

 

따라서, 농도는

 

$\frac{75}{450}\times100≒16.7\%$

 

 

 

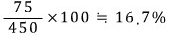
문제7)

20%의 소금물 300g에 10%의 소금물을 섞어

농도가 18%인 소금물을 만들려고 할 때, 넣어야 하는 10%의 소금물의 양은?

 

위의 문제6과 같은 문제인데

그렇게 느껴지나요..?! ;; 암튼

 

20%의 소금물 300g에는 소금이

 

$\frac{20}{100}\times300=60$

 

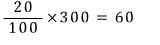
10%의 소금물 ag에는 소금이

 

$\frac{10}{100}\times a=\frac{a}{10}$

 

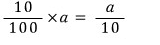
섞으면

 

$소금은\;(60+\frac{a}{10})g$

$소금 물은\;(300+a)g$

 

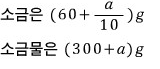
이제 농도 구하는 식을 써보면

 

$\frac{60+\frac{a}{10}}{300+a}\times100=18\quad\rightarrow\quad a=75g$

 

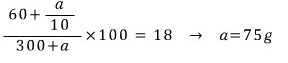
여러분은 이 방정식을 어케 푸는지 모르겠지만

저는 이렇게 푼답니다.

 

일단 번분수 없애주고

 

$\begin{aligned}&\frac{(60+\frac{a}{10})\times10}{(300+a)\times10}\times100=18\\&\frac{600+a}{3000+10a}\times100=18\end{aligned}$

 

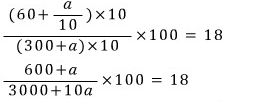
양변에 (3000+10a)를 곱해주고

 

$100(600+a)=18(3000+10a)$

 

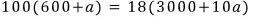
양변을 2로 나눠주고

 

$50(600+a)=9(3000+10a)$

 

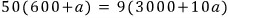
풀면

 

$a=75g$

 

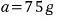
확인 한번 해볼까요

 

20%의 소금물 300g에는 소금이

 

$\frac{20}{100}\times300=60$

 

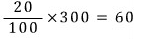
10%의 소금물 75g에는 소금이

 

$\frac{10}{100}\times75=7.5$

 

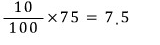
섞으면

 

$소금은\;60+7.5=67.5g$

$소금물은\;300+75=375g$

 

따라서, 농도는

 

$\frac{67.5}{375}\times100=18\%$

 

 

 

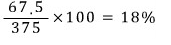
문제8)

20%의 소금물 300g이 들어있는 그릇에서

xg의 소금물을 퍼내고 50g의 물을 넣었더니 15%의 소금물이 되었다. 이 때 x의 값은?

 

처음에 들어있던 소금의 양은

 

$\frac{20}{100}\times300=60$

 

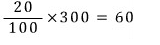
퍼낸 xg에 녹아있는 소금의 양은

 

$300:60=x:a\quad\rightarrow\quad a=\frac{x}{5}$

 

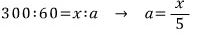
따라서, 남아있는 소금의 양은

 

$60-\frac{x}{5}$

 

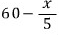
소금물 xg을 퍼내고, 물 50g을 넣었으니

소금물의 양은

 

$(300-x)+50=350-x$

 

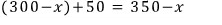
이제 농도 구하는 식을 써보면

 

$\frac{60-\frac{x}{5}}{350-x}\times100=15\quad\rightarrow\quad x=150g$

 

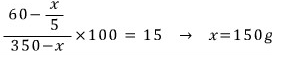
문제7과 같은 방식으로 풀었슴다~

 

$\begin{aligned}&\frac{(60-\frac{x}{5})\times5}{(350-x)\times5}\times100=15\\&\frac{300-x}{1750-5x}\times100=15\\&100(300-x)=15(1750-5x)\\&20(300-x)=3(1750-5x)\\&풀면\\&x=150g\end{aligned}$

 

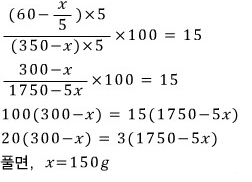
역시 확인을 해보면

 

처음에 들어있던 소금의 양은

 

$\frac{20}{100}\times300=60$

 

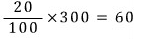
퍼낸 150g에 녹아있는 소금의 양은

 

$\frac{20}{100}\times150=30$

 

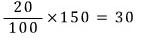
사실 뭐... 계산할 것도 없이

 

300g에서 절반인 150g을 퍼냈으니

소금도 60g의 절반인 30g이 빠져나갔겠죠..?!

 

암튼 그래서

남아있는 소금의 양은

 

$60-30=30g$

 

소금물 150g을 퍼내고, 물 50g을 넣었으니

소금물의 양은

 

$(300-150)+50=200g$

 

따라서, 농도는

 

$\frac{30}{200}\times100=15\%$

 

 

 

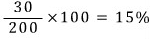
소금물의 농도를 구하는 문제는

소금이나 물을 넣고 빼면서 얼마든지 복잡하게 만들 수 있지만

풀이 방식은 거의 똑같습니다. 동의하죠..?! ;;

 

위의 문제들은 소금을 예로 들었지만 소금이든 뭐든

이제 농도 구하는 문제가 나오면

맘 편히 문제를 풀 수 있을 거라 믿습니다~ ^-^//

 

 

 

▶ 수학 전체 목록 바로가기  →  www.gajok.co.kr/math.html