등비수열의 n항까지의 합은

간단하죠..? ;;;;;
문제1)
첫째항이 3이고, 공비가 2인
등비수열의 20번째항까지의 합은?
걍 공식에 갖다 넣으면 되죠

뭐... 더 할 것도 없습니다.
문제2)
첫째항이 3이고, 공비가 1/2인
등비수열의 20번째항까지의 합은?
역시 공식에 갖다넣으면
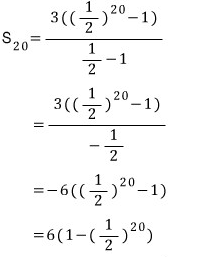
그런데
공비가 1보다 작을 때는

그래서 아래 공식에 다시 넣어보면
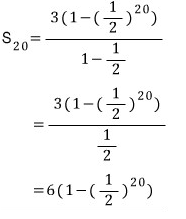
편리함이
느껴지는지 모르겠네요... ;;;;;
공비가 음수일 때는
그 편리함이 확연히 느껴집니다.
한번 해 볼께요...
문제3)
첫째항이 3이고, 공비가 -1/2인
등비수열의 20번째항까지의 합은?

이번에는

식은 한줄 밖에 안 줄었지만
직접 풀어보면 많이 편리할 거예요~
문제4)

등비수열이고
첫째항 2, 공비 2, 항수 20이므로

문제5)
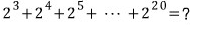
등비수열이고
첫째항 8, 공비 2, 항수 18이므로

문제6)
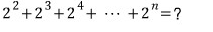
등비수열이고
첫째항 4, 공비 2, 항수 (n-1)이므로
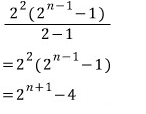
문제7)

등비수열이고
첫째항 16, 공비 2, 항수 (n-2)이므로

문제8)

일단 등비수열이고
첫째항 4, 공비 4
항수는
딱 봐도 10 이란 걸 알 수 있지만
그래도 식으로 풀어야겠죠?
지수만 보면
2, 4, 6, ... , 20
첫째항 2, 공차 2인 등차수열이므로
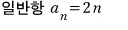
20=2n → n=10
20은 10번째 항..!! 그래서 항수는 10
이제 답을 구해보면
등비수열이고
첫째항 4, 공비 4, 항수 10이므로

답을 이렇게 써도 됩니다~

문제9)
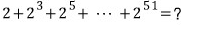
일단 등비수열이고
첫째항 2, 공비 4
지수만 보면
1, 3, 5, ... , 51
첫째항 1, 공차 2인 등차수열이므로

51=2n-1 → n=26
51은 26번째 항..!! 그래서 항수는 26
이제 답을 구해보면
등비수열이고
첫째항 2, 공비 4, 항수 26이므로

역시 답을 이렇게 써도 됩니다~

문제10)
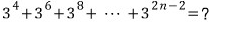
일단 등비수열이고
첫째항 81, 공비 9
지수만 보면
4, 6, 8, ... , (2n-2)
첫째항 4, 공차 2인 등차수열이므로

n에 (n-2)를 대입해야
(2n-2)가 나오므로 → 2(n-2)+2=2n-2
항수는 (n-2)
이제 답을 구해보면
등비수열이고
첫째항 81, 공비 9, 항수 (n-2)이므로

문제11)

일단 등비수열이고
첫째항 243, 공비 9
지수만 보면
5, 7, 9, ... , (2n+1)
첫째항 5, 공차 2인 등차수열이므로

n에 (n-1)을 대입해야
(2n+1)이 나오므로 → 2(n-1)+3=2n+1
항수는 (n-1)
이제 답을 구해보면
등비수열이고
첫째항 243, 공비 9, 항수 (n-1)이므로

시그마로 나온 문제는
다음 글에서 따로 다룰 예정이지만
그래도 미리 잠깐... ;;;;;
문제12)

응?
문제10과 같은 문제입니다..!!
문제10과 꼭같이 풀면되는데
식이 복잡해서 그런지
다르게 푸는 학생들이 있습니다.
이렇게요...

풀이 방법의 선택이야
여러분의 몫이지만
제 입장에서는 권할 수가 없는 풀이입니다. ㅠ
사실 이 문제는

첫째항 81, 공비 9, 항수 (n-2)를 확인하고
이렇게 바로 풀어야 합니다.

에궁... 안 보인다구요?
그럼 아직 공부를 덜 한 거예요... ;;;;;
문제13)

이번에는 눈치채셨나요?
문제11과 같은 문제입니다..!!
역시
이 문제를 다르게 푸는 학생들이 있습니다.

저는
권하지 않는 풀이라고 얘기 했구요...

첫째항 243, 공비 9, 항수 (n-1)

위에서 말씀드렸듯이
시그마는 다음에 자세히(?) 다룰 거예요~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 그래프 읽기 (1) (0) | 2020.06.01 |
|---|---|
| 반원의 방정식 (0) | 2020.05.26 |
| 두 직선의 교점을 지나는 직선의 방정식 (2) (1) | 2020.05.08 |
| 두 직선의 교점을 지나는 직선의 방정식 (1) (0) | 2020.05.08 |
| 접선의 방정식 (2) (0) | 2019.06.24 |