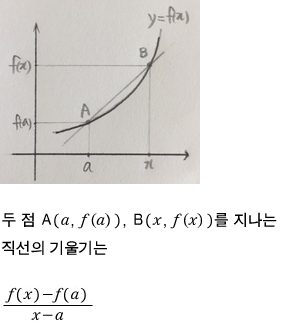
점 B를 점 A쪽으로 이동시켜 볼까요
점 B가 점 A쪽으로 한없이 가까이 가면
즉, x가 a로 한없이 가까이 가면
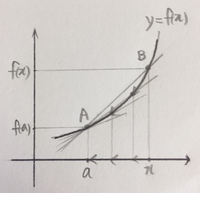
두 점 A, B를 지나는 직선은
결국에는 점 A에서의 접선이 되지 않을까요..?! ;;;;;
식으로 써보면 요렇게 되고
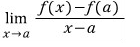
이 식이 의미하는 것은
점 A에서의(x=a 에서의) 접선의 기울기..!!
이 식을 간단하게 f'(a)라고 쓰고
x=a 에서의 미분계수라고 부릅니다.
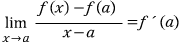
이번에는
x값의 간격을 h로 놓습니다.
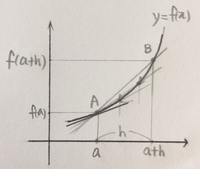
점 B가 점 A쪽으로 한없이 가까이 간다는 것은
h가 0으로 간다는 의미겠죠..?!
그래서, 위의 식이 이렇게 바뀝니다.
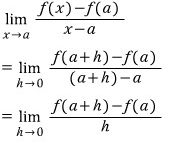
많이 보던 식이죠..?! 암튼 그래서
x=a 에서의 미분계수를 표현하는 식은
요렇게 2개입니다.
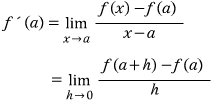
예를 들어
x=2 에서의 미분계수는(접선의 기울기는)
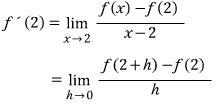
간단한 함수로 한번 연습해 보겠습니다.
문제1)

다른 식으로 구해보면
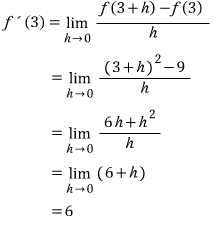
그런데, 사실 미분계수를 처음 공부할 때나
이렇게 번거롭게 구하지
뒤에 가면
그냥 간단히 도함수를 이용해서 미분계수를 구합니다. 요렇게요
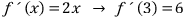
문제2)

문제1과 같은 문제임다~
PS.
미분계수와 도함수(미분함수)를 구분해 보면
f'(x): f(x)의 도함수(미분함수)
f'(2): x=2 에서의 미분계수
f'(x)를 x에서의 미분계수라고 해도 뭐 딱히 틀린 말은 아니지만
f'(2)를 x=2 에서의 도함수라고 하면 좀 이상합니다.
도함수의 정확한 정의는
"정의역의 모든 x에 대해
함수 f(x)의 미분계수로 대응시키는 새로운 함수를 f(x)의 도함수라고 한다."
수학이 어려운 건지
국어가 어려운 건지... ㅎ~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.
