
이 식에서
이항정리의 기본적인 4개의 공식(?)이 나옵니다.
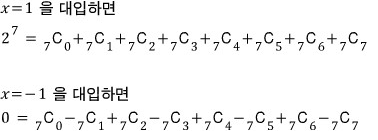
위의 두 식을 더하면
홀수항(?)이 다 사라지고
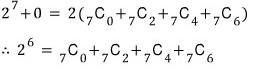
위의 두 식을 빼면
짝수항(?)이 다 사라집니다.

정리해보면
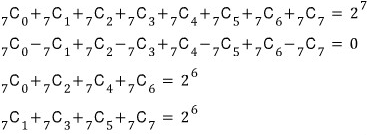
참고로
항의 개수가 짝수일 때는
위와 같이 짝수항, 홀수항이 반반으로 나눠지지만
항의 개수가 홀수일 때는
짝수항의 개수가 하나 더 많습니다.
예를 들어

별로 중요한 내용은 아니니까
한 번 읽고 그냥 넘어가세요~
이제 수학책에 나와 있는
일반식으로 써보면
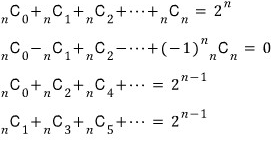
눈에 들어오나요..?!
이외에도
해괴망측한(?) 이항정리 공식이 몇 개 더 있는데
심심치 않게 등장하는 공식
하나만 더 보면
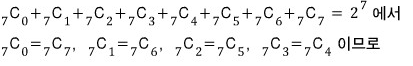
앞의 항 4개의 합과
뒤의 항 4개의 합은 똑같습니다.
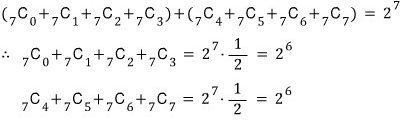
항의 개수가 홀수일 때는
가운데 항을 넘겨주고 생각하면 됩니다. 요렇게

답답한가요..?!
눈 크게 뜨고 자알~ 보는 수 밖에 없슴돠 ;;;;;
이제 문제 하나하나 풀어봅시다~
문제1)
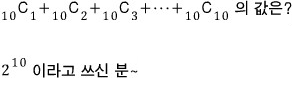
틀리셨습니다..!!

따라서, 답은
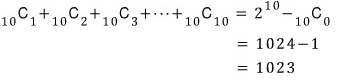
수학공식은 정확하게 알고 잘~ 봐야 합니다.
여차하면 출제자에게 바로 낚입니다.
예를 몇 개 더 들어보면

문제2)

0 이라고 쓰신 분~
틀리셨습니다..!!

따라서, 답은

문제를 살짝 바꿔서

문제3)

아래 전개식에 걍
x=3 을 대입한 것입니다.

따라서, 답은
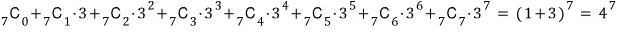
참고로

식의 앞뒤(첫항과 끝항)를 잘 확인하세요~
똑같은 식이여도
거꾸로 적어놓으면 또 달라보입니다. ㅠ

많이 보고 눈에 익히는 수 밖에
달리 방법이 없습니다. 퐛팅..!!
문제4)
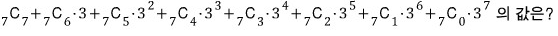
아래 두 식은 같습니다.

문제3은 첫 번째 식에
문제4는 두 번째 식에
x=3 을 대입한 것입니다.
따라서, 답은 똑같습니다.

근데
두 식이 왜 같냐구요..?!
조합의 성질을 이용해서 이해해도 되고
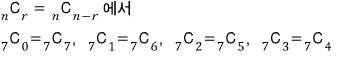
위에서 공식 유도할 때
이미 이 성질을 이용했었죠..?!
아니면
이항정리의 성질(?)을 이용해서 이해해도 됩니다.
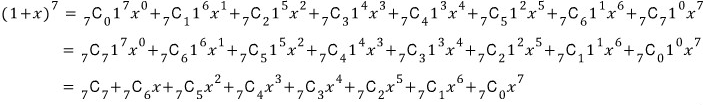
이해가 잘 안 되면 '이항정리 (1)'을 참고하세요~
그래도 지금은 이항정리를 공부하고 있으니까
이항정리의 성질을 이용해서 이해하는 걸로 ;;;;;
역시 참고로

이항정리에서 앞뒤 확인..!!
잊지마세요~
거꾸로 한 번 적어볼까요

이것저것 복잡한 것 같아도 딱 2개입니다.
정리해보면

이걸로도 충분히 머리 아픈데
쌤들은 한 번 더 꼬죠 ㅠ

흐흐흐
머리가 마니마니 아프죠 ;;;;;
사실 저도 이런 거 나올 때마다
많이 헷갈리고 머리가 지끈거립니다.
힘내세요~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 조건부확률 (1) (0) | 2022.08.23 |
|---|---|
| 이항정리 (3) (0) | 2022.08.09 |
| 이항정리 (1) (0) | 2022.07.12 |
| 조합과 순열 (5) (0) | 2022.06.27 |
| 조합과 순열 (4) (0) | 2022.06.14 |