아홉 개의 숫자 1, 2, 3, 4, 5, 6, 7, 8, 9 를 나열하는 경우의 수는?

아홉 개의 숫자 1, 1, 2, 3, 4, 5, 6, 7, 8 을 나열하는 경우의 수는?
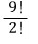
아홉 개의 숫자 1, 1, 2, 2, 2, 3, 4, 5, 6 을 나열하는 경우의 수는?

아홉 개의 숫자 1, 1, 2, 2, 2, 3, 3, 3, 3 을 나열하는 경우의 수는?

느낌 오죠..?!
왜 위와 같이 계산하는지는 여러분이 한 번 생각해 보세요~
생각하기 싫으면
걍 그런가보네하고 넘어가도 상관없구요(?) ;;;;; 암튼
이런 순열의 제목은 '같은 것이 있는 순열'인데 (중복순열과는 달라요)
'같은 것이 있는 순열'의 대표격인 문제가 최단거리 문제입니다.
문제1)
A에서 B까지
최단거리로 가는 경우의 수는?

여기서 최단거리라 함은
한 번 오른쪽으로 갔으면 다시 왼쪽으로 오지 못하고
한 번 위로 올라갔으면 다시 아래로 내려오지 못한다는 의미입니다.
오른쪽 왼쪽 왔다갔다
위 아래 오르락내리락 할 수 있으면
거리가 무한대가 되어버립니다.
이제 여러가지 방법으로
경우의 수를 세어보겠습니다.
풀이1)
오른쪽으로 한 칸 가는 것을 a
위쪽으로 한 칸 가는 것을 b 로 나타내면
A에서 B까지 어떻게 가든지
a는 5개, b는 3개가 나옵니다.
예를 들어
이렇게 가면 baaababa

이렇게 가면 aaabbaab

이런 식으로 생각하면
A에서 B까지 최단거리로 가는 경우의 수는
a, a, a, a, a, b, b, b 를
나열하는 경우의 수와 같게 됩니다.
따라서, 답은
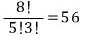
풀이2)
점을 한 번 잡아보겠습니다. 요렇게
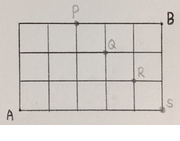
이 점들은 아무렇게나 잡은 게 아니고
중요한 규칙에 따라 잡은 것입니다.
중요한 규칙이란
A에서 B까지 갈 때
1. 이 점들 중 반드시 한 점만을 지나야 하고
2. 이 점들을 지나지 않고 가는 길이 존재해서는 안 된다.
위의 그림을 보면... 어떻게 가든
P, Q, R, S 중 한 점만을 지나며 (예를 들어, P와 Q를 동시에 지날 수는 없습니다.)
P, Q, R, S 중 어느 한 점도 지나지 않고 모두 피해서 가는 길은 없습니다.
이해가 되는지 모르겠네요 ;;;;;
보통은 점들을 대각선으로 잡으면 이 규칙을 만족하게 됩니다.
이제 답을 구해보면
A → P → B 로 가는 경우의 수
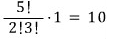
A → Q → B 로 가는 경우의 수
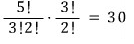
A → R → B 로 가는 경우의 수

A → S → B 로 가는 경우의 수
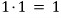
따라서, 답은
10 + 30 + 15 + 1 = 56
연습하는 셈치고
점들을 다르게 잡아서 한 번 구해보겠습니다.
6 + 30 + 20 = 56 (자세한 계산은 여러분이...)

덧붙이면... 대각선을
가는 방향(A에서 B)으로 잡으면 안 돼요~
35 + 30 + 30 + 35 = 130

이렇게 되면
두 점을 동시에 지나서 B까지 갈 수도 있고
세 점을 동시에 지나서 B까지 갈 수도 있고
네 점을 동시에 지나서 B까지 갈 수도 있습니다.
규칙위반입니다..!!
이야기 꺼리가 자꾸 생기네요
풀이2 설명은 여기까지
풀이3)
풀이3은 설명이 없습니다. ㅠ
여러분이 직관적으로 이해하세요~ ;;;;;
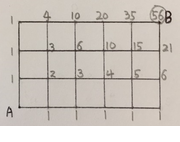
이걸 초등학생 때 배웠다는 학생들도 있는 것 같은데
도대체 초등학교 어느 부분에서..?! 암튼
다른 문제들을 위해서
가는 방향을 바꿔서도 적어보겠슴다.

마지막 그림에
군데군데 화살표를 그려놨는데
이해에 도움이 될랑가요..?! ;;;;;
10+10=20, 5+10=15, 1+5=6, 6+15=21, 21+35=56
사실 이런 깔끔한(?) 길은 걍 풀이1로 풀면 됩니다.
굳이 풀이2, 풀이3으로 풀 필요가 없죠
그런데, 길이 군데군데 끊어져 있으면
풀이1은 쫌 그렇습니다(?)
그래서, 이 때는 대부분 풀이2나 풀이3으로 풉니다.
특히, 풀이3은 마니마니 편리합니다.
풀이1은 끊어진 길이 없는 깔끔한 길에서만 써먹는 걸로...
문제2)
A에서 B까지
최단거리로 가는 경우의 수는?

풀이1)
길이 끊어지지 않고
모든 길이 있다고 가정하면

A에서 B까지 최단거리로 가는 경우의 수는

여기에서
A → C → D → B 로 가는 경우의 수와

A → E → B 로 가는 경우의 수를

빼주면 됩니다.
따라서, 답은

풀이2)
이번에는
가는 길목을 잡아보겠습니다.

이렇게 잡으면
C, D, E, F 중 한 점만을 지나며 (예를 들어, C와 D를 동시에 지날 수는 없습니다.)
C, D, E, F 중 어느 한 점도 지나지 않고 모두 피해서 가는 길은 없습니다.
이제
각각의 경우의 수를 구해보면
A → C → B 로 가는 경우의 수

A → D → B 로 가는 경우의 수

A → E → B 로 가는 경우의 수

A → F → B 로 가는 경우의 수

따라서, 답은

풀이3)
이번에는 설명없는(?) 숫자쓰기..!!

이해가 잘 되지 않으면
친구들이랑 머리를 한 번 맞대보세요~
저는 어케 설명할 방법이... ;;;;;
문제3)
A에서 B까지
최단거리로 가는 경우의 수는?
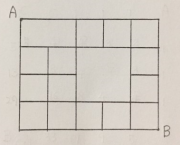
문제2와 똑같은 길이고
출발위치와 도착위치만 바뀌었지만
이런 건 셤에 잘 나오지 않습니다.
너무 어려워서요..!!
어려운 이유는
여러분이 직접 풀어보면 바로 알 수 있을 거예요
그래도 다행인 건... 풀이3은
길의 모양, 출발위치, 도착위치에 상관없이
문제를 쉽게 풀 수 있다는 거..!!
암튼, 아래에 나오는
풀이1과 풀이2는 약식으로만(?) 풀어 놓았으니까요
이해가 잘 되지 않더라도
그냥 그러려니 하고 넘어가세요~ ;;;;;
대신에
풀이3은 완벽히 이해해야겠죠..?!
풀이1)
길이 끊어지지 않고
모든 길이 있다고 가정하면

A에서 B까지 최단거리로 가는 경우의 수는

여기에서
A → C → D → B 로 가는 경우의 수와 (E는 지나든 말든 관심없음)

A → E → B 로 가는 경우의 수를 (C, D는 지나든 말든 관심없음)
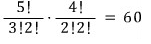
빼주고
A → C → D → E → B 로 가는 경우의 수를

다시 더해주면 됩니다.
따라서, 답은

이해가 안 되죠..?! ㅠ
다른 방식으로 세어보면
A에서 B까지 최단거리로 가는 경우의 수는
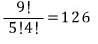
여기에서
A → C → D → B 로 가는 경우의 수와 (E는 지나지 않고)

A → E → B 로 가는 경우의 수와 (C, D는 지나지 않고)

A → C → D → E → B 로 가는 경우의 수를
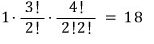
빼주면 됩니다.
따라서, 답은

역시 이해가 잘 안 되죠..?! ㅠ
너무 신경쓰지 마세요~
위에서 말한 것처럼 이런 건 셤에 안 나오니까요
그래도 궁금한 학생들은
한 번 생각해 보세요~
풀이2)
이번에는
가는 길목을 잡아보겠습니다.
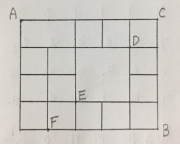
이렇게 잡으면
C, D, E, F 중 한 점만을 지나며 (예를 들어, C와 D를 동시에 지날 수는 없습니다.)
C, D, E, F 중 어느 한 점도 지나지 않고 모두 피해서 가는 길은 없습니다.
이제
각각의 경우의 수를 구해보면
A → C → B 로 가는 경우의 수
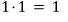
A → D → B 로 가는 경우의 수

A → E → B 로 가는 경우의 수
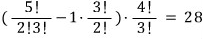
A → F → B 로 가는 경우의 수

따라서, 답은
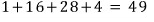
이렇게까지 심오하게(?) 다룰 생각은 전혀 없었는데
기왕에 이렇게 된 거 끝까지 가보죠 뭐...
길목을
다르게 잡아보겠습니다.
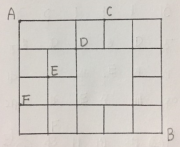
이렇게 잡아도 역시
C, D, E, F 중 한 점만을 지나며 (예를 들어, C와 D를 동시에 지날 수는 없습니다.)
C, D, E, F 중 어느 한 점도 지나지 않고 모두 피해서 가는 길은 없습니다.
이제
각각의 경우의 수를 구해보면
A → C → B 로 가는 경우의 수
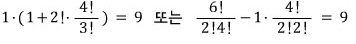
A → D → B 로 가는 경우의 수
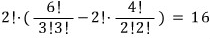
A → E → B 로 가는 경우의 수

A → F → B 로 가는 경우의 수

따라서, 답은

저는 할만큼 했습니다~ ㅎ
역시 궁금한 학생들만 한 번 생각해 보세요~
풀이3)
이번에는 설명없는(?) 숫자쓰기..!!

역시 이해가 잘 되지 않으면
친구들이랑 머리를 한 번 맞대보세요~
저는 어케 설명할 방법이 없슴다. ;;;;;
문제4)
A에서 B까지
최단거리로 가는 경우의 수는?
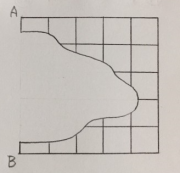
저는 숫자쓰기로만 풀겠습니다.
풀이1, 풀이2 방식은 여러분의 몫으로 남겨 둘께요~ ㅎ
암튼 그래서, 구해보면
이렇게 한 방에 구해도 되고

따로따로(?) 구해서 곱해도 되구요

제가 할 일은 끝난 거 같슴다.
이제는 여러분이 문제집에 나와 있는
다양한 길들을 놓고 한 번 구해보세요~
끄으으으읏~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 이항정리 (1) (0) | 2022.07.12 |
|---|---|
| 조합과 순열 (5) (0) | 2022.06.27 |
| 조합과 순열 (3) (0) | 2022.05.30 |
| 조합과 순열 (2) (0) | 2022.05.16 |
| 조합과 순열 (1) (0) | 2022.05.02 |