정규분포

 

 

 

문제1)

정규분포 문제는 대부분

이 문제처럼 이항분포에서 시작하고

 

풀이는 뭐... 걍

순서를 따라가면 됩니다.

 

① 이항분포를 정규분포로 바꾸고

 

그림을 그려보면 이런 상황입니다.

② 표준화하고

 

그림을 그려보면 이런 상황입니다.

③ 마지막으로 답을 구하는 것은

여러분이 각자 알아서 하는 걸로... ;;;;;

 

정규분포 문제풀이는 (이해를 하든 말든)

이 순서만 따라가면 거의 대부분의 문제가 해결됩니다.

 

 

 

문제2)

확률질량함수를 보면

 

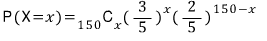
음... 이런 이항분포가 머리에 떠오르나요..?

 

떠오르면 다행이고

안 떠오르면 '이항분포 (2)' 고고~

 

결국, 이 문제는

문제1과 같은 문제라는 거..!!

 

 

 

문제3)

역시, 이 문제도

문제1과 같은 문제임다~

 

 

 

문제4)

걍 문제3을 거꾸로 써놓은 것입니다.

다르게 보이나요..?! ㅎ

 

같은 식을 이렇게 주기도 하죠

 

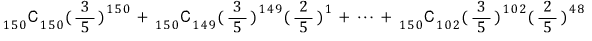
뭐 다른 게 보이나요..?

부디 보이기를... ;;;;;

 

정규분포 이야기는

이걸로 끄읏~ ^-^//

 

 

 

PS1.

정규분포란..?

교과서에 나와 있는 그대로 적어볼께요

 

실수 전체의 집합에서 정의된

연속확률변수 X의 확률밀도함수 f(x)가 두 상수 m, σ (σ＞0) 에 대하여

 

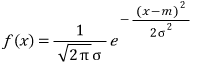
일 때, X의 확률분포를 정규분포라 한다.

 

이 때, 확률밀도함수 f(x)의 그래프는 아래 그림과 같고

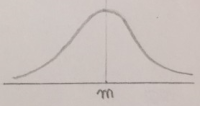
확률변수 X의 평균은 m, 표준편차는  σ임이 알려져 있다.

이 곡선을 정규분포곡선이라 한다.

 

뭐... 그렇다네요... ;;;;;

 

우리는

확률밀도함수 f(x)가 어떻게 생겼는지는 별 관심없고

 

① 그래프가 평균 m을 기준으로 서로 대칭이고

② 그래프와 x축 사이의 넓이는 1이다. (평균선을 기준으로 양쪽으로 0.5씩)

 

요정도만 이해하고 있어도

문제 푸는데는 아무런 지장이 없습니다.

 

 

 

PS2.

정규분포를 표준화 한다는 말은

 

평균 m, 표준편차 σ인 정규분포를

평균 0, 표준편차 1인 표준정규분포로 바꾼다는 의미입니다.

 

어떻게..? 요렇게..!!

 

이 과정을 거치면

 

평균은 0 이 되고

표준편차는 1이 된다고 합니다.

 

평균이 0 이 되는 이유는 알겠는데

 

표준편차가 1이 되는 이유는 잘... ㅠ

누가 아시는 분~ 댓글 좀... ;;;;;

 

아... 그리고 우리는 보통

 

정규분포를 따르는 확률변수는

대부분 X, 상황에 따라 가끔은 다른 문자 Y 등등... 으로 놓고

 

표준정규분포를 따르는 확률변수는

거의 대부분 Z로 놓습니다.

 

표준정규분포를 따르는 확률변수가

Z가 아닌 경우를 저는 본 적이 없습니다. 아직까지는...

 

 

 

PS3.

이항분포를 정규분포로 바꿀 때

 

이런 조건이 붙습니다.

'n이 충분히 크면'

 

교과서에 나와 있는 그대로 적어볼까요

 

확률변수 X가 이항분포 B(n, p)를 따를 때

n이 충분히 크면 X는 근사적으로 정규분포 N(np, np(1-p))를 따른다.

 

충분히 크면..?

n이 얼마면 충분히 큰데..?

 

어떤 수학책을 보면

 

라고 나와있지만

여기도 단서가 붙어 있긴 마찬가지입니다. '일반적으로'

 

결론임다..!!

 

이항분포를 정규분포로 바꿀 때

n이 충분히 큰지 아닌지 따지지 마세요~

 

우리는 그냥

n이 충분히 크다고 가정하고 풀면 됩니다..!!

 

 

 

요기로 가면 → www.gajok.co.kr/math.html

다른 글들도 편리하게 볼 수 있습니다.