아래 수열의 일반항을 구할 수 있나요..?

예전에는 계차수열이란 걸 배웠기때문에
쉽게(?) 구할 수 있었지만... 요렇게요

계차수열을 모르니 이렇게 풀 수는 없고
지금은 살짝 잔머리를 굴려서 풀어야 합니다.
뛰어난 삘(?)을 발휘해서 각 항에 1을 더합니다.

짜잔~ 등비수열이 됐습니다..!!
그럼

여기서 1만 빼주면
처음에 구하려던 수열의 일반항이 나옵니다.

그런데 문제는
이 뛰어난 삘을 어케 발휘하냐는 것입니다.
사실 저도 결과를 알고 1을 더해줬지
딱 보고 안 건 아닙니다. ;;;;;
그래도 너무 걱정할 필요는 없는 게
이런 문제는 셤에 안 나온다는 거
그럼 왜 했냐구요..? 글쎄요...
요정도하고 본론으로 들어갑니다~
이 수열은 공차가 2인 등차수열이고

이 수열은 공비가 3인 등비수열입니다.

그럼 이 수열은요..?

등차수열도 등비수열도 아닌
걍 이름없는 수열이지만
수열의 일반항 구하기에서
대표적으로 나오는 문제입니다.
함 구해볼까요
먼저, 식을 요렇게 변형시켜놓고

α값을 구합니다. 음...

물론
이렇게 놓고 α값을 구해도

α=1 이 돼서
결과는 똑같습니다. 암튼
α값을 찾아 식을 변형했으면

보기 편하게 치환합니다.

그럼 식은 이렇게 되고

등비수열이 등장합니다.
일반항을 구하면

여기서 1만 빼주면
구하려는 수열의 일반항이 나옵니다.
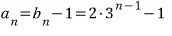
n에 1, 2, 3, 4, 5, ... 를 대입해서
각 항을 구해보면
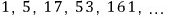
이 글 처음에 나왔던 수열이 나옵니다.
비록 똑같은 수열이지만
현 교육과정에서는
이런 식으로 문제를 주면
일반항을 구할 수 있지만
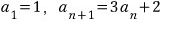
이런 식으로 문제를 주면
일반항을 못 구한다는 거..!!
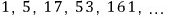
물론 계차수열을 안다거나
뛰어난 삘을 가진 분은 풀 수 있겠지만요 ;;;;;
문제 두 개만 풀께요~
문제1)
아래 수열의 일반항은?
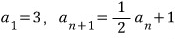
먼저, 식을 요렇게 놓고
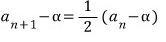
α값을 구하면 α=2
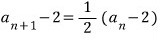
치환하면
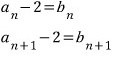
등비수열이 등장하고

여기에 2만 더해주면
처음에 구하려던 수열의 일반항이 나옵니다.
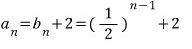
풀 만하죠..?!
문제2)
아래 수열의 일반항은?
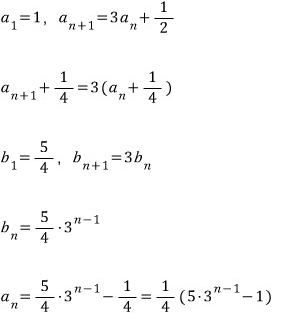
풀이집에는
보통 요정도로만 나와있는데...
천천히 한번 풀어보세요~
PS.
이 수열은 공차가 2인 등차수열이지만
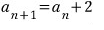
이 수열은 공차가 -2인 등차수열입니다.
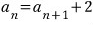
식을 바꾸면 이케 되거든요
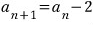
마찬가지로
이 수열은 공비가 3인 등비수열이지만
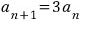
이 수열은 공비가 1/3인 등비수열입니다.
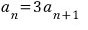
식을 바꾸면 이케 되거든요
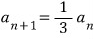
수학쌤들 중에는
가끔 이케 장난치시는(?) 분들이 계십니다.
이런 거에 낚이면 안돼요~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 일반항 (3) (0) | 2021.07.04 |
|---|---|
| 일반항 (2) (0) | 2021.06.27 |
| 등차수열 (1) (0) | 2021.06.13 |
| 분수식의 변형 (3) (0) | 2021.06.06 |
| 분수식의 변형 (2) (0) | 2021.05.30 |