문제1)

x의 내림차순으로 정리하고
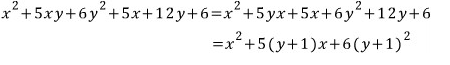
인수분해하면
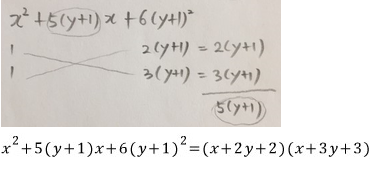
주어진 식이 x, y에 대한 두 일차식
(x+2y+2)와 (x+3y+3)의 곱으로 이쁘게(?) 인수분해 되었습니다.
이해가 안되면 '식의 전개와 인수분해 (3)' 한번 보고 오세요~
이번에는
근의 공식을 이용해서 인수분해를 해보면
역시 x의 내림차순으로 정리하고
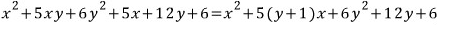
근의 공식에 대입하면
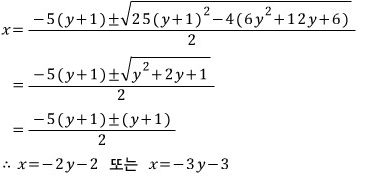
따라서
주어진 식은 다음과 같이 인수분해 됩니다.
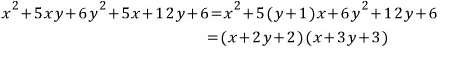
역시 주어진 식이 x, y에 대한 두 일차식
(x+2y+2)와 (x+3y+3)의 곱으로 깔끔하게(?) 인수분해 되었습니다.
이해가 안되면 '식의 전개와 인수분해 (5)' 한번 보고 오세요~
복습은 여기까지하구요
본론으로 들어갑니당~
문제2)

어라?
첫번째 방법으로는 인수분해가 되지 않습니다.
할 수 없죠... 뭐...
근의 공식으로 가야죠 ㅠ
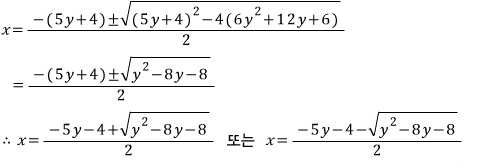
따라서
주어진 식은 다음과 같이 인수분해 됩니다.
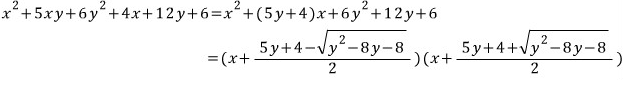
헉! 이게 뭐냐구요?
넘 걱정마세요~ 설마 이딴(?) 문제가 나오겠어요..? ;;;;; 암튼
진짜 본론으로 들어갑니다.
문제1에서 주어진 식은 x, y에 대한 두 일차식의 곱으로 인수분해가 되고
문제2에서 주어진 식은 x, y에 대한 두 일차식의 곱으로 인수분해가 되지 않습니다.
그럼 왜?
문제1에서 주어진 식은 x, y에 대한 두 일차식의 곱으로 인수분해가 되고

문제2에서 주어진 식은 x, y에 대한 두 일차식의 곱으로 인수분해가 되지 않는 걸까요..?
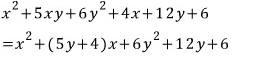
두 식을 방정식으로 생각하고 근을 구해보면 각각
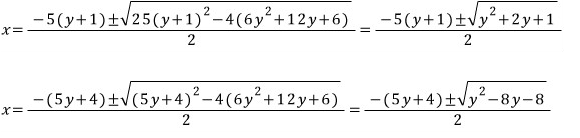
문제1은 루트안에 있는 식이 완전제곱식이 되서 루트가 없어지고
문제2는 루트안에 있는 식이 완전제곱식이 되지 않기 때문에 루트가 없어지지 않습니다..!!
루트 안에 있는 식은 주어진 식의 판별식이고
바로 그 판별식이 완전제곱식이 되야 (즉, 판별식이 0이 되야)
주어진 식이 x, y에 대한 두 일차식의 곱으로 인수분해가 되는 것입니다.
그래서 이런 공식이 나옵니다.
"판별식의 판별식이 0이 되야
x, y에 대한 두 일차식의 곱으로 인수분해 된다."
확인해 보겠습니다.

판별식의 판별식이 0이 되기 때문에
주어진 식이 x, y에 대한 두 일차식의 곱으로 인수분해가 된 것이고

판별식의 판별식이 0이 되지 않기 때문에
주어진 식이 x, y에 대한 두 일차식의 곱으로 인수분해가 되지 않은 것입니다. 휴~
실제 시험문제는 이렇게 나오죠
문제3)

x내림차순으로 정리하고

이 0이 되어야 하므로 a=5
물론 뛰어난 통찰력(?)으로 이렇게 풀어도 됩니다.
풀이집에도 대부분 이렇게 풀어놨구요
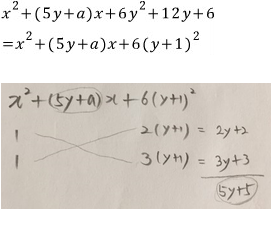
5y가 나오려면
위와 같이 인수분해 하는 수 밖에 없습니다.
따라서, a=5
아래 문제도 뛰어난 통찰력으로 풀리나요..?
문제4)

일단 내림차순으로 정리는 해놓고
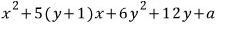
음... 6과 12를 보니
a는 6일 거 같은 삘~
a에 6을 대입해서 한번 시도해 볼만한가요..?
이런 찍기신공은 셤볼 때 하구요
지금은 제대로(?) 풀어야겠죠..? ;;;;;

이 0이 되어야 하므로 a=6
통찰력이 통할 여지는 점점 줄어듭니다.
문제5)

역시 일단은 내림차순 정리

a에 뭐 넣어볼까
고민하고 있는 거 아니죠..?
저는 판별식 바로 들어갑니다~

이 0이 되어야 하므로
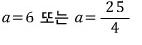
어라?
a값이 2개가 나오네요
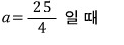
진짜루 x, y에 대한 두 일차식의 곱으로 인수분해 되는지
확인만하고 끝낼께요~
주어진 식에

와우~
진짜루 인수분해가 되네요~ 끄읏~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 식의 전개와 인수분해 (8) (0) | 2020.08.17 |
|---|---|
| 식의 전개와 인수분해 (7) (0) | 2020.08.14 |
| 식의 전개와 인수분해 (5) (0) | 2020.08.07 |
| 식의 전개와 인수분해 (4) (0) | 2020.08.06 |
| 식의 전개와 인수분해 (3) (0) | 2020.08.05 |