문제1)

풀이1)
걍 인수분해해서 구하면 되죠.. 뭐..
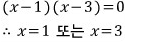
풀이2)
완전제곱식으로 바꿔서 푸는 방법도 있죠
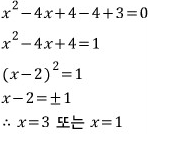
문제2)

갠적으로는... 답을 이렇게 쓰는 것보다
요렇게 따로따로 쓰는 걸 좋아합니다.

문제3)

따로따로 쓰면

잠깐 한마디 하면
제가 공부할 때는 이렇게 근이 허근이 나오면
답안지에는 '근이 없다'라고 적었던 것 같은데
요즘은 근이 실근이든 허근이든
그냥 나오는대로 적는 것 같습니다.
여담이니 걍 잊으세요~
(관심이 있으면 '방정식의 근' 참고요~)
문제4)

따로따로 쓰면

문제5)

a, b, c에 겁먹은 거 아니죠..?!
갑니다~

따로따로 쓰면

마니마니 보던 식이죠
이것이 그 유명한(?) 근의 공식입니다.
근을 구할 때마다 완전제곱식으로 고쳐서 풀기 귀찮으니까
공식으로 만들어 놓고 그냥 써먹는 거죠
외우기 싫다구요..?
상관없습니다.
매번 완전제곱식으로 고쳐서 풀면 되니까요
하지만, 번거로움과 귀찮음은 여러분의 몫입니다. ;;;;;
문제6)

식을 보면 뭘 하려는지 감이 오죠..?!
짝수공식 한번 끄집어 내보려구요
쪼금(?) 간단합니다.

따로따로 쓰면

역시 마니마니 보던
근의 짝수공식입니다.
어떤 쌤들은 헷갈린다고
짝수공식은 사용하지 말라고 하십니다.
그냥 근의 공식 하나만
확실하게 외워서 사용하라고
하지만 저는 결사반대요~
b가 짝수일 때는... 무조건 짝수공식..!!
짝수공식을 사용하는 학생과 그렇지 않은 학생은
서로 레벨이 같을 수가 없습니다. 암튼
이제는 근의 공식을 알았으니
위에서 완전제곱식으로 푼 문제들을
근의 공식으로 풀어보고 마무리 짓겠슴다~
위의 문제1)

짝수공식... 한번 써볼까요
b를 2로 나누면 b'입니다.

그런데 이 문제와 같이 인수분해가 되는 식을 굳이
근의 공식이나 완전제곱식으로 풀 필요는 없죠
근의 공식이나 완전제곱식은
인수분해가 되지 않을 때 써먹는 것입니다.
그리고 완전제곱식은 잘 사용하지도 않습니다.
해봐서 알겠지만 번거롭거든요
완전제곱식은 그냥
이렇게 하는 거구나하는 정도로만 알고 있으면 됩니다.
앞으로는 근을 구하라는데 인수분해가 안된다..?!
그럼 무조건 근의 공식입니다..!!
어..? b가 짝수네
그럼 무조건 짝수공식이구요..!!
한말씀 더...
인수분해가 안되는 줄 알고
열심히 근의 공식에 대입해서 구했는데
답이 그냥 유리수로 나왔다. (즉, 답에 루트가 없다)
그럼 이 식은 인수분해가 되는 식입니다.
예를 들어

근의 공식에 넣어 보면

답에 루트가 없네요
그럼 이 식은
12와 13으로 인수분해가 된다는 소립니다. 이렇게

인수분해가 되는 식을
근의 공식에 대입해서 구했다고 너무 억울해 할 필요는 없는 거 같습니다.
다른 한편으로 생각해보면
이게 뭘로 인수분해되지 하면서 고민할 시간에
걍 근의 공식으로 구하는 것도 좋은 방법일 거 같지 않나요..?! ;;;;;
물로 식을 딱 보고
바로 인수분해를 할 수 있으면 젤 좋죠
에궁... 글이 이상하게(?) 자꾸 길어지네요 ;;;;;
빨리 마무리 짓겠슴다~
위의 문제2)

위의 문제3)
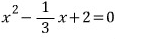
양변에 3을 곱해서 분수를 먼저 없애고 시작합니다.
완전제곱식하고는 반대(?)죠..?!

위의 문제4)

그냥 근의 공식으로도 풀어보면
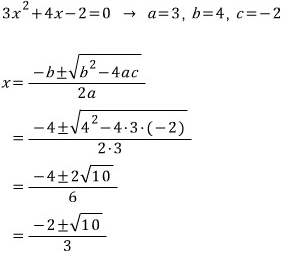
답은 똑같이 나오지만
짝수공식을 강력 권장합니다..!! 끝~~~ ^-^//
▶ 수학 전체 목록 바로가기 → www.gajok.co.kr/math.html
'수학' 카테고리의 다른 글
| 이차방정식의 해 (3) (0) | 2020.09.07 |
|---|---|
| 이차방정식의 해 (2) (0) | 2020.09.03 |
| 방정식의 근 (0) | 2020.08.31 |
| 식의 전개와 인수분해 (11) (0) | 2020.08.24 |
| 식의 전개와 인수분해 (10) (0) | 2020.08.21 |