문제1)

다르게 풀어보면

두 번째 풀이도 뭐 나쁜 건 아니지만
갠적으로 권하지는 않습니다. ;;;;;
문제2)

일단
헷갈림을 방지하기 위해서

이제 풀어보면

이해는 되는 거죠..?!
문자가 등장해서 그렇지
문제1과 똑같은 소릴하고 있는 겁니다.
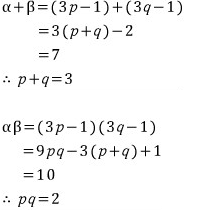
지금은 첨이니까 이해하려고
이렇게 자세히(?) 풀었지만
좀 익숙해 지면
식을 바로 쓰고 바로 풉니다.
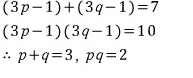
좀 더 지나면

대부분의 문제집은 이렇게 풀어놨습니다.
이제는 풀이집을 봐도 이해가 되겠죠..?!
잔머리(?) 굴려서
좀 간단하게 풀어볼까요?
음...
두 근의 합이 7, 곱이 10이면
두 근은 2와 5

걍 생각나서 풀어보았습니다. ;;;;;
암튼, 이제 준비는 마쳤습니다.
진짜배기(?) 문제는 지금부터...
문제3)

이제부터는
위에서 풀었던 거와 똑같습니다.

이제 풀어보면

역시 좀 익숙해 지면
식을 바로 쓰고 바로 풉니다.

문제4)
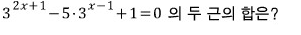
일단 식부터 정리합니다.
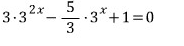
갠적으로 분수가 들어간 식은 안좋아합니다.
양변에 3을 곱하면
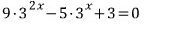
이제부턴 풀 수 있겠죠..?!

문제5)

역시 이제부터는
위에서 풀었던 거와 똑같습니다.

이제 풀어보면

역시 좀 익숙해 지면
식을 바로 쓰고 바로 풉니다.

문제6)
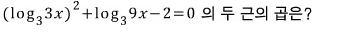
일단 식부터 정리합니다.

마지막 문제입니다.
문제7)
이차방정식 f(2x+3)=0 의 두 근 α, β에 대하여
α+β=4, αβ=7 일 때
이차방정식 f(3x)=0 의 두 근의 합과 곱은?
f(3x)=0 의 두 근을 p, q라고 하면
(2α+3)+(2β+3)=3p+3q
(2α+3)(2β+3)=3p·3q
위의 두 식이 이해가 안 되면 안 돼요. ㅠ
이런 상황이니까 잘 생각해 보세요~
f(x)=0 → ax²+bx+c=0
f(2x+3)=0 → a(2x+3)²+b(2x+3)+c=0
f(3x)=0 → a(3x)²+b(3x)+c=0
답을 구해보면
2(α+β)+6=3(p+q) → p+q=14/3
4αβ+6(α+β)+9=9pq → pq=61/9
▶ 수학 전체 목록 바로가기 → www.gajok.co.kr/math.html
'수학' 카테고리의 다른 글
| 가우스 (0) | 2020.10.05 |
|---|---|
| 이차방정식의 해 (9) (0) | 2020.10.01 |
| 이차방정식의 해 (7) (0) | 2020.09.18 |
| 이차방정식의 해 (6) (0) | 2020.09.16 |
| 이차방정식의 해 (5) (0) | 2020.09.11 |