자취의 방정식 (1)

이 글에 대한 AI '클로드'의 평가

 

(상세한 평가는 이 글 마지막에 있습니다.)

 

 

 

점을 점에 대칭시키거나

 

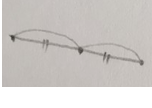
점을 직선에 대칭시킬 때는

 

점 하나만 달랑 대칭시키면 되는데

 

직선을 점에 대칭시킬 때는

직선 위에 있는 무수히 많은 점을 하나씩 하나씩 모두 다 대칭시켜야 합니다.

 

대칭시키는 점을 계속해서 늘리다보면

새로운 도형(이 경우에는 직선)이 생겨납니다.

 

이 도형(직선)이 바로

직선을 점에 대칭시킨 '자취'입니다.

 

그럼 뭐...

이 직선의 방정식이 자취의 방정식이 되겠죠..?!

 

 

 

문제1)

직선 y=2x+1을

점 (4, 2)에 대칭시킨 자취의 방정식은?

 

자취의 방정식은

정해진 순서만 따라가면 간단(?)합니다.

 

먼저

주어진 직선 위의 점들 중

아무점이나 딱 한 점만 대칭시킵니다.

 

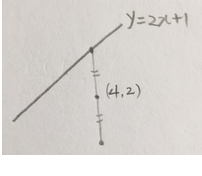
그리고

직선 위의 점을 (a, b)

이 점을 대칭시킨 점을 (x, y)로 놓고

 

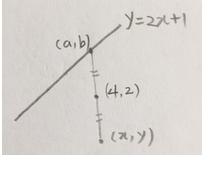
x와 y의 관계식을 구하면

이 식이 바로 자취의 방정식입니다.

 

이제부터의 풀이는

모든 문제집에 나와 있는 풀이 그대로입니다.

 

점 (4, 2)는

두 점 (a, b)와 (x, y)의 중점이므로

 

$\frac{a+x}{2}=4$
$\frac{b+y}{2}=2$

 

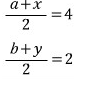
a와 b에 대한 식으로 각각 정리하면

 

$a=8-x$

$b=4-y$

 

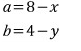
그리는 점 (a, b)는

직선 y=2x+1 위의 점이므로

 

$b=2a+1$

 

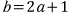
이제 이 식에

위에서 구한 a, b를 대입하고

 

$4-y=2(8-x)+1$

 

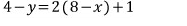
정리하면

 

$y=2x-13$

 

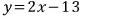
이 놈이 바로

우리가 구하려는 자취의 방정식입니다.

 

자취의 방정식..!!

어렵지 않습니다. 동의하죠..?! ;;

 

 

 

자취의 방정식과는 관련이 없지만

처음에 언급한

 

점을 점에 대칭시킨 점

점을 직선에 대칭시킨 점도 구해볼께요~

 

 

 

문제2)

점 (2, 5)를 점 (3, -1)에 대하여 대칭이동한 점의 좌표는?

 

대칭이동한 점의 좌표를 (a, b)로 놓으면

 

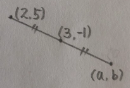
(3, -1)은

두 점 (2, 5)와 (a, b)의 중점입니다.

 

$\frac{2+a}{2}=3 \;\;\rightarrow\;\; a=4$
$\frac{5+b}{2}=-1 \;\;\rightarrow\;\; b=-7$

 

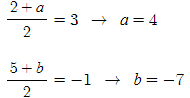
따라서

대칭이동한 점의 좌표는 (4, -7)

 

 

 

문제3)

두 점 (4, 1)과 (-2, 5)가 점 P에 대하여 대칭일 때

점 P의 좌표는?

 

점 P는 두 점 (4, 1)과 (-2, 5)의 중점이므로

점 P의 좌표는 (1, 3)

 

 

 

문제4)

점 (-1, 5)를 직선 3x-y-2=0 에 대하여 대칭이동한 점이 좌표는?

 

대칭이동한 점의 좌표를 (a, b)로 놓으면

 

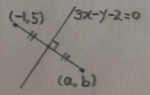
두 점 (-1, 5)와 (a, b)의 중점의 좌표는

 

$\left(\frac{a-1}{2}, \;\frac{b+5}{2}\right)$

 

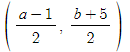
직선 3x-y-2=0 위의 점이므로

대입하고 정리하면

 

$3\left(\frac{a-1}{2}\right)-\left(\frac{b+5}{2}\right)-2=0$

$3a-b=12$

 

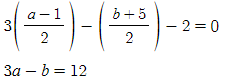
그리고

 

직선 3x-y-2=0은 기울기가 3이고

두 점 (-1, 5)와 (a, b)를 이은 선분과 수직이므로

 

두 점 (-1, 5)와 (a, b)를 이은 선분의 기울기는 $-\frac{1}{3}$

 

$\frac{b-5}{a+1}=-\frac{1}{3}$

$a+3b=14$

 

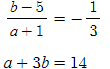
두 식을 연립해서 풀면

$a=5, \;\;b=3$

 

따라서

대칭이동한 점의 좌표는 (5, 3)

 

 

 

▶ 수학 전체 목록 바로가기  →  www.gajok.co.kr/math.html