728x90
반응형
이차함수(곡선)를 점에 대칭시키면
곡선이 나오겠죠..?!
그림은 엉성하지만
대충 이런 모양이 나올 듯요
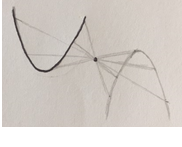
문제)

앞에서 (자취의 방정식 (1))
자취의 방정식은 어떻게 구한다고 했죠?
많이도 필요없고
아무점이나 딱 한점만 대칭시킵니다.
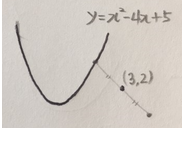
그리고
곡선 위의 점을 (a, b)
이 점을 대칭시킨 점을 (x, y)로 놓고
x와 y의 관계식을 구합니다.
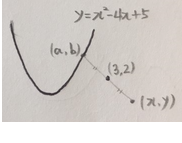
구해보면
점 (3, 2)는
두 점 (a, b), (x, y)의 중점이므로
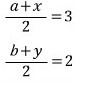
a와 b에 대한 식으로 각각 정리하면

그리고... 점 (a, b)는

이 식에
위에서 구한 a, b를 대입하고
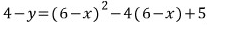
정리하면

이 놈이 바로
우리가 구하려는 자취의 방정식입니다.
그런데
이차함수의 특성상(?) 다르게 구하기도 하죠
주어진 이차함수의 꼭지점 (2, 1)을

(3, 2)에 대칭시키면
(4, 3)이 나옵니다.
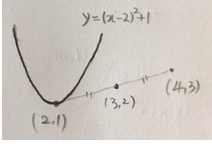
어케 구하냐구요?
여러분이 직접 구해보세요~ ;;;;;
암튼... 이 (4, 3)이
자취의 방정식의 꼭지점이 되고

자취의 방정식의
이차항의 계수는 부호만 바꿔서 -1
정리하면
우리가 구하려는 자취의 방정식은
꼭지점의 좌표는 (4, 3)이고
이차항의 계수가 -1인 이차함수..!!

처음에 식으로 구한 것과 결과가 같습니다.
당연히..!! ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

728x90
반응형
'수학' 카테고리의 다른 글
| 자취의 방정식 (4) (0) | 2020.10.16 |
|---|---|
| 자취의 방정식 (3) (0) | 2020.10.14 |
| 자취의 방정식 (1) (0) | 2020.10.08 |
| 가우스 그래프 (0) | 2020.10.07 |
| 가우스 (0) | 2020.10.05 |