문제)

점 P를 (a, b)
점 Q를 (x, y)로 놓고 시작합니다.

점 Q는 선분 AP를 2:1로 내분하는 점이므로

a와 b에 대한 식으로 각각 정리하면

이 식에
위에서 구한 a, b를 대입하고
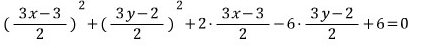
정리하면
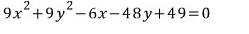
식을 바꿔보면
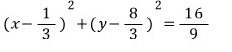
이 놈이 바로
우리가 구하려는 자취의 방정식입니다.
그런데 이 문제를
대칭시킨 자취의 방정식을 구할 때처럼 (자취의 방정식 (3))
주어진 원의 중심의 좌표를 구하고 (-1, 3)

(3, 2)와 (-1, 3)을 2:1로 내분하는 점을 구해서

이렇게 구하면 안돼욧..!!
대칭시킬 때는
처음 그래프와 자취의 그래프의 반지름이 같지만
내분할 때는
처음 그래프와 자취의 그래프의 반지름이 달라지거든요..!!
다시 말해
처음 주어진 원의 반지름이 2라고 해서

우리가 구하려는
자취(원)의 반지름도 2라는 보장이 없다는 말씀..!!
위에서 구한 답(자취의 방정식)을 보면

반지름의 길이가
2가 아니라 4/3인 걸 확인할 수 있습니다.
이것저것 헷갈리면
대칭시킨 자취의 방정식이든
내분한 자취의 방정식이든
그냥
자취의 방정식을 구하는 순서대로 구하면 됩니다.
괜히 조금 편하려다가
틀리는 것보단 낫잖아요... ;;;;;
그래도 난 곧 죽어도
다른 방법으로 구해야겠다면
원 위에 아무 점이나 하나잡고
내분점을 구합니다.
(1, 3)을 잡으니 (5/3, 8/3) 이 나오네요
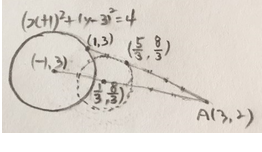
그럼
우리가 구하려는 자취의 방정식은

따라서
우리가 구하려는 자취의 방정식은
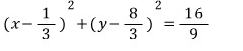
처음에 구한 자취의 방정식과 같습니다..!!
뭐... 지금까지 설명을 하긴했지만
여기까지 하나하나 이해하면서 따라오신 분이 계실라나..? ;;;;;
사실 자취의 방정식을
이렇게까지 자세히 이해할 필요는 전혀(?) 없습니다.
여러분은
기본개념과 풀이만 정확히 이해하고 문제를 풀면 됩니다.
이런 잔머리를 동원한 편법적인(?) 풀이는
나중에요~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 자취의 방정식 (8) (0) | 2020.10.28 |
|---|---|
| 자취의 방정식 (7) (0) | 2020.10.27 |
| 자취의 방정식 (5) (0) | 2020.10.21 |
| 자취의 방정식 (4) (0) | 2020.10.16 |
| 자취의 방정식 (3) (0) | 2020.10.14 |