728x90
반응형
문제1)

점 P를 어디에 찍어야
주어진 조건을 만족하는지는 알 수 없으니까
그냥 아무데나 찍고 만족한다고 가정합니다.
그리고... (x, y)로 놓기

이제 뭐... 식만 쓰면 됩니다.

정리하면
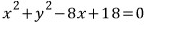
문제2)

역시 점 P를 어디에 찍어야
주어진 조건을 만족하는지는 알 수 없습니다.
그냥 P(x, y)로 놓고
식을 만들면 끝입니다.
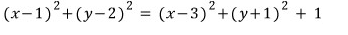
정리하면
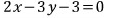
문제3)

P(x, y)라 놓고 식을 만들면

양변 제곱하고 정리하면
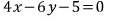
그런데 지금 이 경우는
조건을 만족하는 점 P의 위치를 찾을 수가 있습니다.

이 그림을 보고 식을 세워도 똑같습니다.

그리고 조건을 만족하는 점 P를 더 찾아보면
결국은 선분 AB의 수직이등분선이 됩니다.
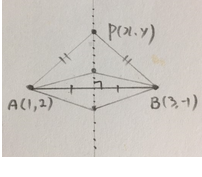
그래서 문제집에서는 이 문제를
선분 AB의 수직이등분선의 방정식을 구해서 풀기도 합니다.

정리하면
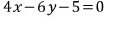
결과가 같습니다.
여러분은 어떤 풀이가 더 편할지 모르겠네요
맘에 드는 걸로 푸세요~
문제4)
두 점 A(1, 2), B(3, -1)에 대하여
선분 AB를 수직으로 이등분하는 직선의 방정식은?
문제3과 같은 문제입니다. ;;;;;
문제5)
두 점 A(1, 2), B(3, -1)에 대하여
두 점에 이르는 거리가 같은 점들의 자취의 방정식은?
역시 문제3을 말로 풀어쓴 것 뿐입니다~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

728x90
반응형
'수학' 카테고리의 다른 글
| 자취의 방정식 (9) (0) | 2020.10.29 |
|---|---|
| 자취의 방정식 (8) (0) | 2020.10.28 |
| 자취의 방정식 (6) (0) | 2020.10.23 |
| 자취의 방정식 (5) (0) | 2020.10.21 |
| 자취의 방정식 (4) (0) | 2020.10.16 |