728x90
반응형
문제)
두 점 A(1, 3), B(4, 0)에 이르는 거리의 비가 2:1인
점 P의 자취의 방정식은?
뭐 딱히 다르지 않습니다.
지금까지 풀어온 그대로 걍 풀면 됩니다.
거리의 비가 2:1인 점 하나만 찍고
(x, y)로 놓고 식을 만들면 끝~
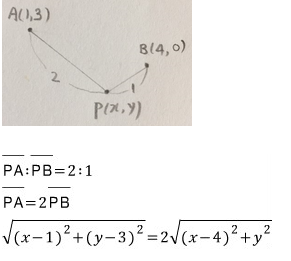
양변 제곱해서 정리하면

다르게 풀기도 하죠
사실 거리의 비가 2:1인 점은 무수히 많고
계속 찍다보면 원이 나타납니다.

그 중에서 특히 직선 AB 위에 있는 점을
우리는 내분점, 외분점이라고 부르고 (→ '내분점과 외분점' 참고)
우리가 구하려는 자취는
바로 이 내분점과 외분점을 지름의 양끝으로 하는 원이 됩니다.
아폴로니우스의 원이라고 하나요? 뭐 암튼...
그래서 구해보면
내분점은 (3, 1)
외분점은 (7, -3)
원의 중심은 (5, -1)


따라서 우리가 구하려는 자취의 방정식은

어떤 풀이가 더 맘에 드나요?
전 내분점, 외분점, 원의 중심, 반지름 구하는 게 귀찮아서(?)
걍 식으로 푸는 것을 좋아한답니다~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

728x90
반응형
'수학' 카테고리의 다른 글
| 자취의 방정식 (11) (0) | 2020.11.02 |
|---|---|
| 자취의 방정식 (10) (0) | 2020.10.30 |
| 자취의 방정식 (8) (0) | 2020.10.28 |
| 자취의 방정식 (7) (0) | 2020.10.27 |
| 자취의 방정식 (6) (0) | 2020.10.23 |