x를
x로, y로, t로 각각 미분해 보겠습니다.

감이 잡히나요..? ;;;;;
이번에는 y를 미분해 볼께요~

이번에는 x, y 같이 있는 거...

원의 방정식을 배울 때
걍 외운 이런 공식이 하나 있었습니다.

이제 합성함수의 미분도 알았으니
한번 유도해 볼께요~

그리고

따라서
우리가 구하려는 접선의 방정식은

문제1)
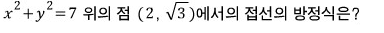
공식에 대입하면
답은 뭐... 걍 나옵니다.
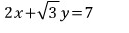
그래도 한번 미분해서 구해보겠습니다.
배웠으니까 ;;;;;

문제2)
시각 t초에서의 반지름이 3t이면
5초일 때, 원의 넓이의 순간변화율은?
시각 t초에서의 반지름이 3t란 소리는
반지름은 매초 3씩 커진다는 소리입니다. 암튼...
원의 넓이를 S라 놓으면

양변을 t로 미분하면

따라서, t=5 일 때
원의 넓이의 순간변화율은

그런데 풀이집을 보면
대부분 조금 다르게(?) 풀어놓았죠

양변을 t로 미분하면

따라서, t=5 일 때
원의 넓이의 순간변화율은
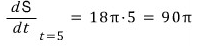
문제3)
시각 t초에서의 반지름이 (3t+2)이면
5초일 때, 구의 겉넓이와 부피의 순간변화율은?
구의 겉넓이를 S, 부피를 V라 하면

양변을 t로 각각 미분하면

따라서, t=5 일 때
구의 겉넓이와 부피의 순간변화율은 각각
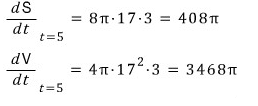
에궁... 숫자가 너무 크네요 ㅠ
그래도 풀이집에 나온대로 풀어봐야겠죠...

양변을 t로 각각 미분하면

따라서, t=5 일 때
구의 겉넓이와 부피의 순간변화율은 각각

요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 두 직선의 교점을 지나는 직선의 방정식 (1) (0) | 2020.05.08 |
|---|---|
| 접선의 방정식 (2) (0) | 2019.06.24 |
| 접선의 방정식 (1) (0) | 2019.06.17 |
| 합성함수의 미분 (0) | 2019.06.13 |
| 함수 (6) (0) | 2019.06.13 |