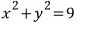
한번 그려볼께요
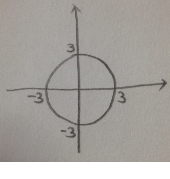
이제 한번 생각해 보겠습니다.

그리고 9는
이 원의 반지름의 제곱입니다.
너무 당연한 소릴했나요..?!
한걸음 살짝 앞으로 나갑니다.
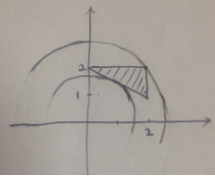
아래 그림에서
주어진 영역에 속하는 점들 중에
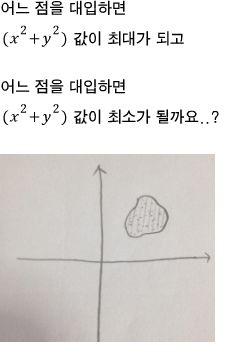
찬찬히 한번 생각해 보겠습니다.
아무렇게나 하나만 그려볼께요
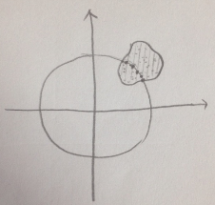
그럼
이 원 위에 걸리는 점들의

하나 더 그려볼까요

이 원 위에 걸리는 점들의

감 잡았나요..?
문제로 돌아와서... 그럼

바로
점 A를 지날 때
가장 큰 원이 그려져서 최대가 되고
(최댓값은 이 때 생기는 원의 반지름의 제곱입니다.)
점 B를 지날 때
가장 작은 원이 그려져서 최소가 됩니다..!!
(최솟값은 이 때 생기는 원의 반지름의 제곱입니다.)

나름 열심히 설명했는데
이해가 됐는지 모르겠네요 ;;;;;
주어진 영역에 속하는 점 (x, y)에 대하여

문제1)

(2, 2)를 지날 때
가장 큰 원이 그려지고 (최댓값이 되고)
(0, 2)와 (2, 1)을 지나는 직선에 접할 때
가장 작은 원이 그려집니다. (최솟값이 됩니다.)
먼저, 간단한 최댓값부터...
그냥 (2, 2)를 대입해서 구해도 되고
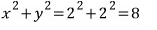
아니면
이 원의 반지름을 구해서 제곱을 해도 됩니다.
반지름은 (0, 0)과 (2, 2)사이의 거리

최솟값은...
(0, 2)와 (2, 1)을 지나는 직선의 방정식은
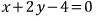
원점에서 이 직선까지의 거리

최솟값을
판별식을 이용해서 구해도 되죠
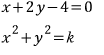
이렇게 놓고
직선과 원이 접할 때(판별식=0)의 k값을 구하면 됩니다.
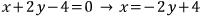
원의 방정식에 대입

최솟값을
또 다르게 한번 구해 볼까요
마찬가지로
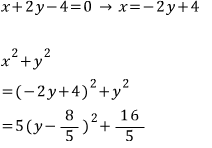
따라서

이렇게 구하니까
최소일 때(접할 때)의 접점의 좌표도 나오네요
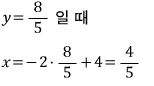
따라서, 접점의 좌표는
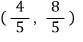
풀이가 너무 많죠..?! ;;;;;
문제2)

문제1과 똑같이

최댓값은
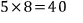
최솟값은
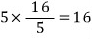
문제3)

문제가 어려워 보이나요..?
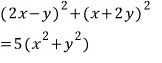
문제2와 똑같은 문제입니다..!!
결국
문제1, 문제2, 문제3이 모두 같은 문제입니다.
문제1은 잘 풀면서
문제2나 문제3은 모르겠다고하면 참 슬프겠죠..?! ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 유리함수 (1) (0) | 2021.02.01 |
|---|---|
| 이차식의 최대최소 (3) (0) | 2021.01.28 |
| 이차식의 최대최소 (1) (0) | 2021.01.21 |
| 일차식의 최대최소 (3) (0) | 2021.01.18 |
| 일차식의 최대최소 (2) (0) | 2021.01.14 |