항등식 (3)

이 글에 대한 AI '클로드'의 평가

 

(상세한 평가는 이 글 마지막에 있습니다.)

 

 

 

문제1)

다음 등식이 x, y에 대한 항등식이 되도록 하는 상수 a, b, c의 값은?

(a+1)x+(b-3)y+c+2=-x+y+5

 

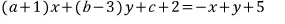
계수를 비교하거나 (계수비교법)

 

a+1=-1, b-3=1, c+2=5

∴ a=-2, b=4, c=3

 

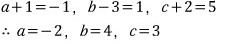
아무 숫자나 대입해서 풀면 됩니다. (수치대입법)

 

x=0, y=0을 대입하면 c+2=5

x=0, y=1을 대입하면 b-3+c+2=6

x=1, y=0을 대입하면 a+1+c+2=4

 

∴ a=-2, b=4, c=3

 

근데, 이 문제를 굳이

수치대입법으로 풀 필요는 없겠죠..?! ;;

 

 

 

문제2)

x-y=2 를 만족시키는 모든 실수 x, y에 대하여

ax²+by²+cxy+x+y+6=0이 성립할 때

상수 a, b, c의 값은?

 

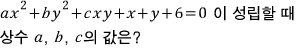
y=x-2이므로 대입하고

ax²+b(x-2)²+cx(x-2)+x+(x-2)+6=0

 

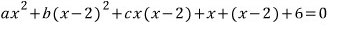
정리하고

(a+b+c)x²+(-4b-2c+2)x+4b+4=0

 

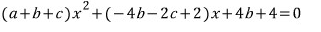
계수비교하면

 

a+b+c=0, -4b-2c+2=0, 4b+4=0

∴ a=-2, b=-1, c=3

 

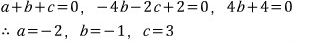
수치대입도 해보면

 

x=0 대입 4b+4=0

x=1 대입 (a+b+c)+(-4b-2c+2)+4b+4=0 정리하면 a+b-c=-6

x=-1 대입 (a+b+c)+(4b+2c-2)+4b+4=0 정리하면 a+9b+3c=-2

 

∴ a=-2, b=-1, c=3

 

역시

수치대입보다는 계수비교가 편하죠..?!

 

확인도 해볼 겸

식을 y에 대한 항등식으로 바꿔볼까요.

 

x=y+2이므로

대입하고 정리하고 계수비교해서 풀면

 

ax²+by²+cxy+x+y+6=0

 

a(y+2)²+by²+c(y+2)y+(y+2)+y+6=0

(a+b+c)y²+(4a+2c+2)y+4a+8=0

 

a+b+c=0, 4a+2c+2=0, 4a+8=0

∴ a=-2, b=-1, c=3

 

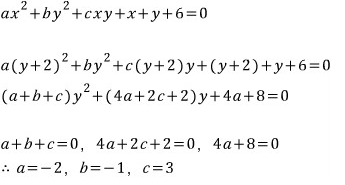
수치대입은 여러분이 해보세요~

뭐... 안 해봐도 딱히 상관 없습니다. ;;

 

암튼, 식을

 

x에 대한 항등식으로 정리해서 푸나 (계수비교든 수치대입이든)

y에 대한 항등식으로 정리해서 푸나 (계수비교든 수치대입이든)

 

아무런 상관이 없습니다.

 

그런데..!!

 

이럴 바엔 아예 첨부터

수치대입하는 것도 좋은 선택이 될 것 같네요.

 

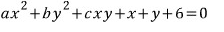
한 가지 주의할 것이 있다면

 

x값, y값을 대입할 때

 

문제1에서는

x값, y값을 서로 상관없이 아무 값이나 내맘대로 대입해도 됐지만

 

이 문제에서는

x-y=2라는 조건이 주어졌기 때문에

이 등식에 맞는 값을 대입해 줘야 된다는 거..!!

 

예를 들어

 

x에 3을 대입하면

y에는 아무 수나 대입하면 안 되고 무조건 1을 대입해야 됩니다.

 

그래야 x-y=2가 되니까요.

 

문제로 돌아와서

 

ax²+by²+cxy+x+y+6=0

 

x=2, y=0 대입 4a+2+6=0

x=0, y=-2 대입 4b-2+6=0

x=3, y=1 대입 9a+b+3c+3+1+6=0

 

∴ a=-2, b=-1, c=3

 

훨씬 편하죠..?!

 

결론입니다.

 

이런 문제는 식을 정리할 필요도 없이

걍 첨부터 수치대입해서 푸는 걸로..!!

(단, 주어진 조건에 맞는 숫자로..!!)

 

 

 

간단한(?) 내용인데

어째 글이 쫌 길어졌네요 ^-^// ;;

 

 

 

▶ 수학 전체 목록 바로가기  →  www.gajok.co.kr/math.html