문제1)

x→1 일 때
분모→0 이고, 극한값이 존재하므로
분자→0 이어야 한다. ('미분계수 (3)' 참고요~)
이 성질을 이용해서 문제를 풀려는데
어라..?! 분자에 1을 대입하니 걍 0 이 되어 버리네요 ㅠ

그래서, 이런 문제는 다르게 풀죠
미분계수의 정의를 이용하기 위해서
억지로 함수를 하나 만듭니다. 요렇게요

그러면 주어진 식은 이렇게 바뀌고

이젠 뭐 그냥 풀면 됩니다.

따라서

바뜨...
우리의 고3들은 이렇게 안 풀고
입가에 미소를 띠며 분모와 분자를 각각 미분해서 풀죠 (로피탈의 정리)

문제2)

풀이1)

따라서, 답은 11/2
풀이2)
로피탈의 정리를 이용해서
분모와 분자를 각각 미분하면

풀이3)
인수분해가 능수능란(?)하면
요렇게 풀 수도 있습니다. ('식의 전개와 인수분해 (9)' 참고요~)

여러분의 수학실력은 어느 정도인가요
위의 세 가지 풀이가 모두 자연스럽게 다가오나요..?! ;;;;;
문제3)
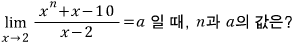
x→2 일 때
분모→0 이고, 극한값이 존재하므로
분자→0 이어야 합니다.

n의 값이 정해졌으니까 이제
나머지 풀이는 문제2와 똑같습니다.
풀이1)

풀이2)
로피탈의 정리를 이용해서
분모와 분자를 각각 미분하면

풀이3)
굳이 인수분해를 해서 풀어보면

에궁... 글을 다 쓰고보니
'식의 전개와 인수분해 (9)'의 내용과 살짝(?) 겹치네요 ㅠ
복습한 셈치죠... 뭐... ^-^// ;;;;;
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 접선의 방정식 (4) (0) | 2022.02.10 |
|---|---|
| 접선의 방정식 (3) (0) | 2022.02.04 |
| 미분계수 (3) (0) | 2022.01.15 |
| 미분계수 (2) (0) | 2021.12.28 |
| 미분계수 (1) (0) | 2021.12.12 |