절댓값이야기입니다.
l3l=3, l-3l=3 이건 잘 아는데
lal가 뭐냐고 물으면 잘 모릅니다. ㅠ
절댓값 안에 있는 값이 양수이면
그냥 나오면 되고
l3l=3
절댓값 안에 있는 값이 음수이면
그냥 나온 후에, 마이너스를 붙여주면 됩니다.
l-3l은 먼저 -3을 쓴 후에
앞에 마이너스를 붙여줍니다. 요렇게
l-3l=-(-3)=3
그래서
l-3l=3 이 되는 것입니다.
많은 학생들은 그냥 마이너스를 없애고 쓰면 된다고 생각하고 있지만
절댓값 안에 있는 것이 숫자가 아니라 문자면 곤란해집니다.
그럼 lal의 값을 생각해 보겠습니다.
lal는 a의 값이 뭔지 모르기 때문에 그 때 그 때 값이 달라집니다.
ⅰ) a가 양수이면 (a>0)
lal는 그냥 절댓값 기호를 없애고 a라고 쓰면 됩니다.
lal=a
ⅱ) a가 음수이면 (a<0)
lal는 먼저 절댓값 기호를 없애고 a라고 쓴 후에
앞에 마이너스를 붙여주면 됩니다.
lal=-a (참고로, 여기서 -a는 양수입니다. a가 음수인데 앞에 마이너스가 붙었으니까요)
ⅲ) a가 0이면 (a=0)
lal는 a라고 쓰든, -a라고 쓰든, 0이라고 쓰든, -0이라고 쓰든 아무런 상관이 없습니다.
a=-a=0=-0 모두 같잖아요
그래서 경우를 위와 같이 세가지로 나누지 않고
보통은 두가지로 나눕니다.
ⅰ) a≥0 일 때, lal=a
ⅱ) a<0 일 때, lal=-a
또는
ⅰ) a>0 일 때, lal=a
ⅱ) a≤0 일 때, lal=-a
보통은 등호를 첫번째 경우처럼 양수 쪽에 붙여줍니다.
물론 두번째 경우처럼 음수 쪽에 붙여줘도 상관없습니다.
중요한 것은 양수든 음수든 한쪽에만 붙여줘야 된다는 거..!!
양수에 붙였으면 음수에는 붙이지 말고
음수에 붙였으면 양수에는 붙이지 말고
암튼, 앞으로 우리는 양수 쪽에 붙이겠습니다.
수학은 남들하는대로 따라하는 것이 젤 좋더라구요... ;;;;;
그래서 거의 모든 교과서와 문제집에는
lal의 값을 다음과 같이 표현하고 있습니다.
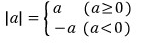
많이 보던 거죠..?!
절댓값은 한가지만 생각하면 됩니다.
절댓값 안에 있는 놈이 양수냐? 음수냐?만 판단하면 되는 것입니다.
쪼금 응용해 볼까요
아... 응용... 수학에서 별로 반갑지 않은 단어죠. 그래도...
la-2l는 어떻게 풀면 될까요
절댓값 안에 있는 놈은 (a-2)입니다.
언제 이 놈이 양수가 됐다, 음수가 됐다 하죠?
그 기준은 2입니다.
a가 2보다 크면
절댓값 안에 있는 (a-2)는 양수가 되고
a가 2보다 작으면
절댓값 안에 있는 (a-2)는 음수가 됩니다.
위의 말을
식으로 표시해보면

(주의: a<2일 때, 꼭꼭꼭 괄호를 치세요. 괄호가 없으면 (-a-2)가 되어 버립니다.)
감을 잡았는지 모르겠네요
몇 개 더 해볼까요?

그럼 lx-yl는..?
지금까지 해온 것처럼 말로 풀어볼께요
lx-yl는
절댓값 안에 있는 (x-y)가 양수이면 그냥 나오고
절댓값 안에 있는 (x-y)가 음수이면 그냥 나오고 나서, 앞에 마이너스를 붙여줍니다.
순서를 바꿔쓰면
lx-yl는
그냥 나오고 (절댓값 안에 있는 (x-y)가 양수이면)
그냥 나오고 나서, 앞에 마이너스를 붙여줍니다. (절댓값 안에 있는 (x-y)가 음수이면)
이 말을
식으로 바꿔만 주면 답입니다.
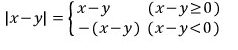
물론 이렇게 써도 됩니다.
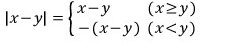
중요한 건
절댓값 안에 뭐가 오든지 간에 (그 식의 의미를 이해하는 것은 나중 문제구요)
그냥 갖다 쓰기만 하면 됩니다.
쫌 과장하면

그냥 이렇게 쓰기만 하면 답입니다.
참 쉽죠... ;;;;;
이제 문제 몇 개 풀어볼께요
중학교 문제인지 고등학교 문제인지 구분은 하지 않겠습니다.
그리고 여러분은 푸는 것이 아니라
걍 읽기만 하면 됩니다. 착하죠..?! ㅎ~
문제1)
lxl=3 을 만족하는 x값은?
l3l도 3이고, l-3l도 3이므로
lxl=3 을 만족하는 x값은 3 또는 -3
사실 이 문제를 간단하게 풀었지만
모든 절댓값 문제의 풀이는
절댓값 안의 값이
양수냐 음수냐를 구분해서 푸는 것이 기본적인 방식입니다.
한번 이런 식으로 풀어보겠습니다.
lxl=3을 만족하는 x값은?
ⅰ) x가 양수이면, lxl=x=3
ⅱ) x가 음수이면, lxl =-x=3 → x=-3
따라서
lxl=3 을 만족하는 x값은 3 또는 -3
잘 봐두기 바랍니다.
이런 풀이에 조금씩 익숙해져야 하니까요. 중요한 풀이입니다..!!
문제2)
lx-2l=3 을 만족하는 x값은?
(x-2)는 3이여도 되고, -3이여도 됩니다. 즉
x-2=3 또는 x-2=-3
따라서, x=5 또는 x=-1
역시 다르게 풀어보면
ⅰ) x가 2보다 크면, (x-2)는 양수이므로 x-2=3 → x=5
ⅱ) x가 2보다 작으면, (x-2)는 음수이므로 -(x-2)=3 → x=-1
굳이 이 문제를 이렇게까지 풀 이유는 없습니다.
하지만 익숙해지라고 두 번이나(?) 반복해서 풀었습니다.
풀이를 꼭 이해해야 합니다.
나중을 위해서..!!
좀 이상한 거 풀어볼까요
lx-3l=-4 를 만족하는 x값은?
절댓값은 음수가 나올 수 없으므로 만족하는 x는 없다. 끝입니다.
괜히 풀려고 노력하지 마세요~
하지만, 역시 다른 방법으로 풀어보겠습니다.
ⅰ) x가 3보다 크면, (x-3)은 양수이므로 x-3=-4 → x=-1
ⅱ) x가 3보다 작으면, (x-3)은 음수이므로 -(x-3)=-4 → x=7
헐... 답이 존재하지 않는데
답이 2개나 나옵니다. 이런... ㅠ
사실 아주 중요함에도 불구하고 위에서 말하지 않은 것이 있습니다.
한꺼번에 설명하면 짜증낼까봐요. 이제 말하려구요 ;;;;;
우리가 이 문제를 풀 때
'x가 3보다 크면'이라는 조건하에 문제를 풀어서
답이 x=-1 이 나온 것입니다.
그럼 나온 답이 조건을 만족하는지 반드시 확인해야 한다는 것입니다.
즉, -1은 'x가 3보다 크면'이라는 조건에 맞지 않으므로 이 답은 버려야 합니다.
두 번째도 마찬가지입니다.
'x가 3보다 작으면'이라는 조건하에 문제를 풀어서
답이 x=7 이 나온 것입니다.
그럼 역시 나온 답이 조건을 만족하는지 반드시 확인해야 합니다.
즉, 7은 'x가 3보다 작으면'이라는 조건에 맞지 않으므로 이 답도 버려야 합니다.
두 개의 답이 모두 조건을 만족하지 않으므로
답이 없는 것입니다.
여러분은 제가 지금 얼마나 중요한 말을 했는지를 모르겠지만(?)
정말로 중요한 내용입니다..!!
이런 원칙은 절댓값 문제뿐만 아니라
모든 수학문제 풀이에 그대로 적용됩니다.
어떠어떠한 조건하에서 문제를 풀어 답이 나왔으면
나온 답이 그 조건을 만족하는지 반드시 확인해야 한다..!!
조건을 만족하면 답이 되고
조건을 만족하지 않으면 미련없이 버려라..!!
그럼 다시 위로 올라가서
lx-2l=3 을 만족하는 x값은?
ⅰ) x가 2보다 크면, (x-2)는 양수이므로 x-2=3 → x=5
ⅱ) x가 2보다 작으면, (x-2)는 음수이므로 -(x-2)=3 → x=-1
첫번째, x=5
'x가 2보다 크면'이라는 조건에 만족하고
두번째, x=-1
'x가 2보다 작으면'이라는 조건에 만족합니다.
따라서
5와 -1 모두 답이 되는 것입니다.
두 개 모두 그대로 답이 되기 때문에
위에서는 말하지 않고 그냥 패스한 것입니다.
처음 문제도 확인해 볼까요
lxl=3 을 만족하는 x값은?
ⅰ) x가 양수이면, lxl=x=3
ⅱ) x가 음수이면, lxl =-x=3 → x=-3
첫번째, x=3
'x가 양수이면'이라는 조건에 만족하고
두번째, x=-3
'x가 음수이면'이라는 조건에 만족합니다.
역시 두 개 모두 조건에 만족하므로
둘 다 답이 됩니다.
어떤 조건하에서 문제를 풀었으면
나온 답이 그 조건을 만족하는지 반드시 확인해야 된다는 거..!!
잊지마세요~~
참고로, 그래프를 이용한 풀이는
'절댓값이 포함된 방정식과 부등식'의 문제1에 있습니다.
문제3)
lx+1l=2x-5 를 푸시오. (수학에서 풀라는 말은 x값을 구하라는 의미입니다.)
lxl=3 이나 lx-2l=3 과 같이
절댓값이 달랑 숫자로만 나오면
굳이 양수니 음수니 생각할 거 없이
걍 아래와 같이 풀면 됩니다.
lxl=3 → x=±3
lx-2l=3 → x-2=±3 → x=5 또는 x=-1
하지만, 이 문제와 같이
숫자만 나오는 것이 아니라
x도 함께 나오면 양수 음수 구분해서 풀어야 합니다.
한번 풀어보겠습니다.
lx+1l=2x-5
ⅰ) x가 -1보다 크면, (x+1)은 양수이므로 x+1=2x-5 → x=6
ⅱ) x가 -1보다 작으면, (x+1)은 음수이므로 -(x+1)=2x-5 → x=4/3
따라서, 답은 x=6 또는 x=4/3
어때요? 쉽죠?
다음 문제를 풀어보겠습니다.
뭐... 할 말 없나요..?!
뜬금없이 뭔소리냐구요..?!
위에서 나온 답이 조건에 맞는지 확인해 봤나요?
아차하는 님들도 많을 것입니다.
확인해 볼까요
첫번째, x=6
'x가 -1보다 크면'이라는 조건에 만족하지만
두번째, x=4/3
'x가 -1보다 작으면'이라는 조건에 만족하지 않습니다.
따라서, 두번째 x=4/3 는 버리고
답안지에는 x=6 만 써야 합니다.
두 개 모두를 썼다면
문제를 다 풀어놓고 틀린 것입니다. ㅠ
다시 거듭거듭 말하지만
조건을 꼭 확인하세요~
문제4)
lx+2l-3x+1=0
ⅰ) x가 -2보다 크면, (x+2)는 양수이므로 x+2-3x+1=0 → x=3/2 (조건에 만족)
ⅱ) x가 -2보다 작으면, (x+2)는 음수이므로 -(x+2)-3x+1=0 → x=-1/4 (조건에 만족하지 않습니다.)
따라서, 답은 x=3/2
문제5)
lx-1l+lx+2l=5
이번에는 절댓값이 2개가 나왔습니다.
절댓값이 1개면, 양수냐 음수냐 기준이 되는 값이 1개인데
절댓값이 2개면, 양수냐 음수냐 기준이 되는 값이 2개입니다.
여기서는 1과 -2입니다.
그럼, 구간은 3개로 나눠집니다.
ⅰ) x>1 이면
(x-1) 양수, (x+2) 양수
따라서, 식은 (x-1)+(x+2)=5 → x=2 (조건에 만족)
ⅱ) -2≤x≤1 이면
(x-1) 음수, (x+2) 양수
따라서, 식은 -(x-1)+(x+2)=5 → 3=5 (식이 성립하지 않습니다.)
이 구간의 어떤 수가 와도 이 방정식을 만족시키지 못합니다.
즉, -2와 1 사이에는 해가 없다는 의미..!!
ⅲ) x<-2 이면
(x-1) 음수, (x+2) 음수
따라서, 식은 -(x-1)-(x+2)=5 → x=-3 (조건에 만족)
따라서, 이 방정식의 해는
x=2 또는 x=-3
참고로, 그래프를 이용한 풀이는
'절댓값이 포함된 방정식과 부등식'의 문제2에 있습니다.
역시 참고로
위에서 구간을 나눌 때 등호를 가운데로 몰아서
x>1, -2≤x≤1, x<-2 이렇게 나눴는데
x≥1, -2<x<1, x≤-2 이렇게 나눠도
x≥1, -2≤x<1, x<-2 이렇게 나눠도
x>1, -2<x≤1, x≤-2 이렇게 나눠도 아무런 상관이 없습니다.
다만, 중요한 것은
등호를 한쪽에만 붙여주라는 것입니다.
x>1 에서 안붙였으면 -2≤x≤1 에는 붙이고
x≥1 에서 붙였으면 -2<x<1 에는 붙이지 말고
x≥1 에 붙였는데 -2≤x≤1 에도 붙이거나
x>1 에 붙이지 않았는데 -2<x<1 에도 붙이지 않으면 안된다는 말씀입니다.
-2도 마찬가지입니다.
대부분의 풀이집에서는 가운데로 몰지 않는데
저는 가운데로 모는 게 편해서 가운데로 몰아서 풀었습니다. ;;;;;
문제6)
lx-1l+lx+2l=3
문제3에서
5가 3으로만 바뀌었습니다. ;;;;;
역시 구간은 3개로 나눠집니다.
ⅰ) x>1 이면
(x-1) 양수, (x+2) 양수
따라서, 식은 (x-1)+(x+2)=3 → x=1 (조건에 만족하지 않습니다.)
ⅱ) -2≤x≤1 이면
(x-1) 음수, (x+2) 양수
따라서, 식은 -(x-1)+(x+2)=3 → 3=3 (식이 성립합니다.)
이 구간의 어떤 수가 와도 이 방정식은 성립합니다.
즉, -2와 1 사이에 있는 모든 수가 해가 된다는 의미입니다..!!
따라서, 해는 -2≤x≤1 에 있는 모든 수
ⅲ) x<-2 이면
(x-1) 음수, (x+2) 음수
따라서, 식은 -(x-1)-(x+2)=3 → x=-2 (조건에 만족하지 않습니다.)
따라서, 이 방정식의 해는
-2≤x≤1 입니다.
이 시점에서 구간을 나누는 것에 의문을 품는 님들이 계실 것 같아서
구간을 다르게 나눠서 풀어보겠습니다.
등호 붙이는 위치를 바꿔본다는 소리입니다.
ⅰ) x≥1 이면
(x-1) 양수, (x+2) 양수
따라서, 식은 (x-1)+(x+2)=3 → x=1 (조건에 만족)
ⅱ) -2<x<1 이면
(x-1) 음수, (x+2) 양수
따라서, 식은 -(x-1)+(x+2)=3 → 3=3 (식이 성립합니다.)
이 구간의 어떤 수가 와도 이 방정식은 성립합니다.
즉, -2와 1 사이에 있는 모든 수가 해가 된다는 의미입니다..!!
따라서, 해는 -2<x<1 에 있는 모든 수
ⅲ) x≤-2 이면
(x-1) 음수, (x+2) 음수
따라서, 식은 -(x-1)-(x+2)=3 → x=-2 (조건에 만족)
따라서, 이 방정식의 해는
-2≤x≤1 로 결과가 같습니다.
참고로, 그래프를 이용한 풀이는
'절댓값이 포함된 방정식과 부등식'의 문제3에 있습니다.
문제7)
lx-3l+l2x+1l-3x=2
문제가 어려워 보이나요?
그래봤자 풀이는 똑같습니다.
절댓값 2개, 기준이 되는 값도 2개 (3과 -1/2)
따라서, 구간은 3개로 나눠집니다.
ⅰ) x>3 이면
(x-3) 양수, (2x+1) 양수
따라서, 식은 (x-3)+(2x+1)-3x=2 → -2=2 (식이 성립하지 않습니다.)
즉, 이 구간에서는 해가 없습니다.
ⅱ) -1/2≤x≤3 이면
(x-3) 음수, (2x+1) 양수
따라서, 식은 -(x-3)+(2x+1)-3x=2 → x=1 (조건에 만족)
ⅲ) x<-1/2 이면
(x-3) 음수, (2x+1) 음수
따라서, 식은 -(x-3)-(2x+1)-3x=2 → x=0 (조건에 만족하지 않습니다.)
따라서, 이 방정식의 해는
달랑 x=1 밖에 없습니다.
문제8)
lx-1l+lx-2l+lx-3l=4
절댓값 3개, 기준이 되는 값도 3개 (1, 2, 3)
따라서, 구간은 4개로 나눠집니다.
ⅰ) x>3 이면
(x-1) 양수, (x-2) 양수, (x-3) 양수
(x-1)+(x-2)+(x-3)=4 → x=10/3 (조건에 만족)
ⅱ) 2<x≤3 이면
(x-1) 양수, (x-2) 양수, (x-3) 음수
(x-1)+(x-2)-(x-3)=4 → x=4 (조건에 만족하지 않습니다.)
ⅲ) 1<x≤2 이면
(x-1) 양수, (x-2) 음수, (x-3) 음수
(x-1)-(x-2)-(x-3)=4 → x=0 (조건에 만족하지 않습니다.)
ⅳ) x≤1 이면
(x-1) 음수, (x-2) 음수, (x-3) 음수
-(x-1)-(x-2)-(x-3)=4 → x=2/3 (조건에 만족)
따라서, 이 방정식의 해는
x=10/3 또는 x=2/3
참고로, 그래프를 이용한 풀이는
'절댓값이 포함된 방정식과 부등식'의 문제4에 있습니다.
문제9)
lxl+y=4
lxl-y=2
ⅰ) x≥0
x+y=4
x-y=2
풀면 x=3, y=1 (조건에 만족)
ⅱ) x<0
-x+y=4
-x-y=2
풀면 x=-3, y=1 (조건에 만족)
따라서, 이 연립방정식의 해는
x=3, y=1 또는 x=-3, y=1
좀 다르게 풀어보면
lxl+y=4
lxl-y=2
두 식을 더하면 2lxl=6 → lxl=3 → x=±3
x=3 이면 y=1
x=-3 이면 y=1
풀이가 짧고 깔끔합니다.
많은 문제집에서도 이렇게 풀어놨구요
하지만, 저는 이런 풀이보다는
첫번째 풀이를 강력히 권장합니다..!!
문제10)
lxl+y=4
l3xl-y=2
ⅰ) x≥0
x+y=4
3x-y=2
풀면 x=3/2, y=5/2 (조건에 만족)
ⅱ) x<0
-x+y=4
-3x-y=2
풀면 x=-3/2, y=5/2 (조건에 만족)
따라서, 이 연립방정식의 해는
x=3/2, y=5/2 또는 x=-3/2, y=5/2
역시 다르게 풀어보면
lxl+y=4
3lxl-y=2 (3을 밖으로 빼도 상관이 없습니다.)
두 식을 더하면 4lxl=6 → lxl=3/2 → x=±3/2
x=3/2 이면 y=5/2
x=-3/2 이면 y=5/2
문제11)
lxl+l3yl=4
l3xl-lyl=6
ⅰ) x≥0, y≥0
x+3y=4
3x-y=6
풀면 x=11/5, y=3/5 (조건에 만족)
ⅱ) x≥0, y<0
x-3y=4
3x+y=6
풀면 x=11/5, y=-3/5 (조건에 만족)
ⅲ) x<0, y≥0
-x+3y=4
-3x-y=6
풀면 x=-11/5, y=3/5 (조건에 만족)
ⅳ) x<0, y<0
-x-3y=4
-3x+y=6
풀면 x=-11/5, y=-3/5 (조건에 만족)
따라서, 이 연립방정식의 해는
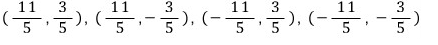
역시 다르게 풀어보면
lxl+3lyl=4
3lxl-lyl=6
풀면
lxl=11/5 → x=±11/5
lyl=3/5 → y=±3/5
따라서, 이 연립방정식의 해는
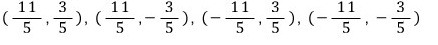
답은 첫번째 풀이와 똑같습니다.
문제12)
lx-2l+2y-5=0
lx+3l-y-4=0
이제부터는 다른 풀이가 없습니다.
오직 기본풀이 뿐입니다.
ⅰ) x>2
(x-2) 양수, (x+3) 양수
(x-2)+2y-5=0
(x+3)-y-4=0
풀면 x=3, y=2 (조건에 만족)
ⅱ) -3≤x≤2
(x-2) 음수, (x+3) 양수
-(x-2)+2y-5=0
(x+3)-y-4=0
풀면 x=5, y=4 (조건에 만족하지 않습니다.)
ⅲ) x<-3
(x-2) 음수, (x+3) 음수
-(x-2)+2y-5=0
-(x+3)-y-4=0
풀면 x=-17/3, y=-4/3 (조건에 만족)
따라서, 이 연립방정식의 해는
x=3, y=2 또는 x=-17/3, y=-4/3
문제13)
lx-yl+2y=8
2x-y=-1
ⅰ) x≥y
(x-y) 양수
(x-y)+2y=8
2x-y=-1
풀면 x=7/3, y=17/3 (조건에 만족하지 않습니다.)
ⅱ) x<y
(x-y) 음수
-(x-y)+2y=8
2x-y=-1
풀면 x=1, y=3 (조건에 만족)
따라서, 이 연립방정식의 해는
x=1, y=3
어떠세요... 풀 만하죠..?!
어디가서 수학이 어렵다는 말은 하지 마세요. 수학은 쉽습니다.
단지 수학이 귀찮고 싫을 뿐...
수학이 나랑 안맞을 뿐...입니다. ㅎ
암튼 여기까지요~ ^-^//
▶ 수학 전체 목록 바로가기 → www.gajok.co.kr/math.html
'수학' 카테고리의 다른 글
| 절댓값 (3) (0) | 2020.07.27 |
|---|---|
| 절댓값 (2) (0) | 2020.07.24 |
| 무연근 (0) | 2020.07.14 |
| 이차부등식의 해 (2) (0) | 2020.06.23 |
| 이차부등식의 해 (1) (0) | 2020.06.08 |