절댓값 (2)

이 글에 대한 AI '클로드'의 평가

 

(상세한 평가는 이 글 마지막에 있습니다.)

 

 

 

 

 

 

문제1)

|x-5|=3x-1을 푸시오.

 

ⅰ) x≥5

x-5=3x-1 → x=-2

 

ⅱ) x<5

-(x-5)=3x-1 → x=3/2

 

∴ x=-2 또는 x=3/2

 

이렇게 풀고 끝내신 분~

답이 틀렸답니다. ;;

 

답은 그냥

x=3/2입니다.

 

이유가 궁금하면 '절댓값 (1)'을 읽어보세요~

저는 걍 넘어갑니다. 

 

 

구간을 나누기 귀찮으면

양변을 제곱해서 풀기도 하죠.

 

|x-5|²=(3x-1)²

 

식을 정리해서 풀면

 

x=-2 또는 x=3/2

 

참고로

절댓값 제곱은 그냥 제곱하는 것과 같습니다.

 

|x-5|²=(x-5)²=x²-10x+25

 

암튼, 이렇게 풀고 끝내신 분~

역시 답이 틀렸답니다. ㅠ

 

x=-2는 무연근이기 때문에

x=3/2만 답입니다.

 

무연근이 뭐냐구요?

역시 궁금하신 분은 '무연근'을 읽고 오세요~

 

이번 글은 읽을 게 많네요. ;;

 

 

 

문제2)

|x-5|=|3x-1|을 푸시오.

 

풀이1)

ⅰ) x>5

x-5=3x-1 → x=-2 (조건에 만족하지 않습니다.)

 

ⅱ) 1/3≤x≤5

-(x-5)=3x-1 → x=3/2 (조건에 만족)

 

ⅲ) x<1/3

-(x-5)=-(3x-1) → x=-2 (조건에 만족)

 

∴ x=3/2 또는 x=-2

 

풀이2)

그냥 제곱해서 풀기

 

|x-5|²=|3x-1|²

(x-5)²=(3x-1)²

2x²+x-6=0

(x+2)(2x-3)=0

∴ x=-2 또는 x=3/2

 

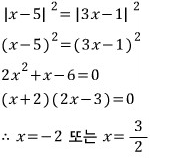
이 때는 무연근이 나타나지 않습니다.

확인해 보세요~ ;;

 

풀이3)

|A|=|B|

이런 꼴의 방정식은 그냥 간단하게

 

A=B 또는 A=-B

이렇게 풀면 됩니다.

 

|x-5|=|3x-1|

이 방정식을 풀라고 하면

 

x-5=3x-1

x-5=-(3x-1)

 

∴ x=-2 또는 x=3/2

 

 

풀이1, 2, 3 중에

어떤 풀이가 맘에 드나요?

 

취향(?)이 특별하지 않다면

풀이3을 선택할 것 같은데... 아닌가요..?! ;;;;;

 

저의 선택은 무조건 풀이3입니다..!!

 

 

참고로

 

이와 관련된 풀이가

점과 직선과의 거리 구하는 식에서 등장합니다.

 

|3x-4y+1|=|4x-3y-5|

 

이 식을 정리하려면 일단

 

풀이1은

어케 안될 거 같고

 

풀이2는

억지로라도 무식하게(?) 정리해보면

 

|3x-4y+1|²=|4x-3y-5|²

(3x-4y+1)²=(4x-3y-5)²

9x²+16y²+1-24xy+6x-8y=16x²+9y²+25-24xy-40x+30y

7x²-7y²-46x+38y+24=0

7x²-46x-(7y²-38y-24)=0

7x²-46x-(y-6)(7y+4)=0

{x+(y-6)}{7x-(7y+4)}=0

(x+y-6)(7x-7y-4)=0

∴ x+y-6=0 또는 7x-7y-4=0

 

풀이 중간에 나오는 인수분해가 이해가 안되면

'식의 전개와 인수분해 (3)' 참고요~

 

이제 풀이3으로 풀어보면

 

|3x-4y+1|=|4x-3y-5|

3x-4y+1=4x-3y-5 또는 3x-4y+1=-(4x-3y-5)

∴ x+y-6=0 또는 7x-7y-4=0

 

누가 풀이3을 선택하지 않으리오..?! ^-^//

 

 

 

 

 

 

 

▶ 수학 전체 목록 바로가기  →  www.gajok.co.kr/math.html