'일차함수 (1)' 마지막 부분에서 잠깐 다뤘는데
그래도 확인하고 갈께요
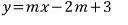
이 함수를 보고 알 수 있는 것은..?
일단
기울기가 m인 직선이고
m으로 묶으면

이 직선은 m값에 관계없이
(2, 3)은 무조건 지나는 직선이라는 거..!!
그래서
y=mx-2m+3 을 그리라고 하면
기울기가 정해지지 않았기 때문에
어떻게 그려도 상관없지만
(2, 3)은 반드시 지나게 그려야 한다는 거..!! 요렇게

앞에서 한 거 기억나죠..?! ;;;;;
문제1)

문제집에서 흔히 볼 수 있는 문제지만
일차함수가 부실한 학생에게는 많이 어려울 수 있습니다.
일단
y=-x+3 부터 그려놓고

이제는 다른 직선이

(-1, 2)를 지나면서
제1사분면에서 만나도록 그리면 됩니다.
그렇게 되려면
(0, 3)을 지날 때를 경계로는
아래로 내려와야 하고
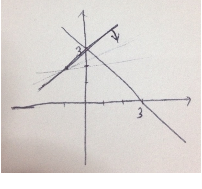
(3, 0)을 지날 때를 경계로는
위로 올라가야 합니다.

이제
각각의 경우에 m값을 구하면 됩니다.
먼저
(0, 3)을 지날 때의 m값은
y=mx+m+2 에
(0, 3)을 대입 → m=1
간단히
기울기를 이용해서 구해도 되죠
(-1, 2)와 (0, 3)을 지나므로
기울기 m=1
암튼
(0, 3)을 지날 때의 m값은 1입니다.
다음으로
(3, 0)을 지날 때의 m값을 구하면
y=mx+m+2 에
(3, 0)을 대입 → m=-1/2
기울기를 이용해서 구해도 똑같이 나옵니다.
여러분이 확인해 보세요~
따라서
두 직선이 제1사분면에서 만나기 위한 m값의 범위는

'일차함수 (1)'의 문제8과 같은 유형입니다.
의도치않게 복습을 했네요 ;;;;;
문제2)

두 그래프를 그려보면

문제1과 그림은 똑같지만
m값은 다릅니다..!!
(0, 3)을 지날 때
3=2m·0+2m+2 → m=1/2
(3, 0)을 지날 때
0=6m+2m+2 → m=-1/4
따라서, m값의 범위는

이렇게
좌표를 대입해서 구하면 아무런 문제가 없는데
기울기를 이용해서 구하려면
주의해야 합니다.
y=2mx+2m+2 의 기울기는
m이 아니라 2m이기 때문입니다.
(-1, 2)와 (0, 3)을 지날 때의 기울기는 1
m=1 이 아니라 2m=1 입니다. → m=1/2
(-1, 2)와 (3, 0)을 지날 때의 기울기는 -1/2
m=-1/2 이 아니라 2m=-1/2 입니다. → m=-1/4
따라서, m값의 범위는

이제 아래 두 직선의
공통점과 차이점이 보이나요..?

두 직선 모두 (-1, 2)를 똑같이 지나지만
기울기는 서로 다르다는 거..!! 주의하세욧..!!
문제3)

두 그래프를 그려보면

그림이 도대체 뭐냐구요..?!
나름 최선입니다. ;;;;;
일차함수 2개일 때는
교점의 좌표를 이용해서 구했는데
일차함수, 이차함수일 때는
판별식을 이용해서 구합니다.

두 그래프가 서로 접하므로 D=0 에서
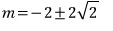
따라서, 두 그래프가 서로 만나려면
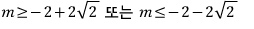
참고로, 두 그래프가 서로 만나지 않으려면

기울기가 크고 작고가 헷갈리면
'일차함수 (1)'을 살짝 한번 들여다 보세요~
문제4)

역시 그림을 먼저 그립니다.
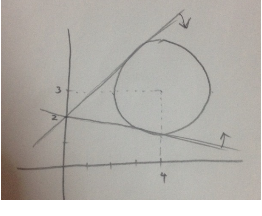
풀이가 2가지가 있죠..?!
판별식과 점과 직선과의 거리
판별식은 귀찮으니까(?)
점과 직선과의 거리를 이용해서 구할께요
원의 중심 (4, 3)에서
직선 mx-y+2=0 까지의 거리가
원의 반지름 2와 같을 때의 m값을 구합니다.

따라서, 두 그래프가 서로 만나려면

역시 참고로
두 그래프가 서로 만나지 않으려면

문제5)

일단 상황부터 파악해보면
일차함수는

m값에 관계없이
(1, 2)를 지나는 직선이고
무리함수야
다 그릴 줄 아실거고... ;;;;;
그래서 그래프를 그려보면
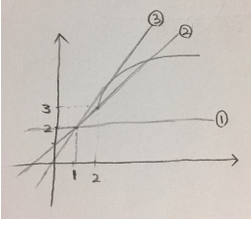
직선 ①일 때는 기울기가 0이므로
m=0
직선 ②일 때는 (2, 3)을 지나므로
y=mx-m+2 에 대입 → m=1
직선 ③일 때는 접하므로
(판별식=0)을 이용해서 구하면 될 듯요

에궁... 식을 복잡하게 만들어 놨네요
어쩔 수 없슴다. 그냥 갑니다~
양변을 제곱하고

정리하면

이 경우 m은 양수..!!

휴~ 이런 식
한번 풀어보는 것도 나쁘진 않죠..?! ;;;;;
답을 정리해보겠습니다.

잘 한번 생각해 보세요~
아래 문제6은 좀 어려우니
이해가 잘 안되더라도 너무 신경쓰지 말고 걍 무시하세요~
문제6)

이 그래프는

중심 (4, 3), 반지름 2인
윗쪽 반원이라는 것이 보이나요..?
안 보이면 '반원의 방정식' 참고요~
일단 그림부터

직선 ①일 때는 (6, 3)을 지나므로
y=mx-m+2 에 대입 → m=1/5
직선 ②일 때는 (2, 3)을 지나므로 역시
y=mx-m+2 에 대입 → m=1
직선 ③일 때는 구해볼께요
(4, 3)에서
mx-y-m+2=0 에 이르는 거리는 2

음수는 버리고

정리해보면

에궁... 괜히 했나요..?! ;;;;;
이런 문제 셤에 안 나오니까
위에서도 말했듯이 걍 무시하세요~ ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.
