분수식을
세 가지 경우로 나눠 보았습니다.
① 분모가 일차식인 경우
② 분모가 이차식인 경우 (인수분해 되는)
③ 분모가 이차식인 경우 (인수분해 안 되는)
중간중간에 식의 변형이 잘 안 되면
'분수식의 변형 (1), (2), (3)'을 참고하세요~
① 분모가 일차식인 경우
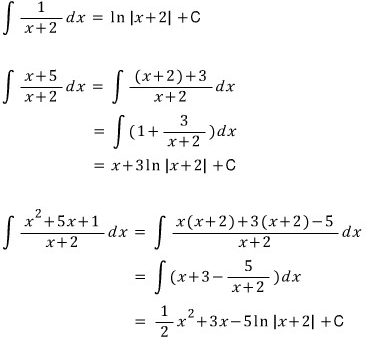
② 분모가 인수분해 되는 이차식인 겨우

여기까지야 뭐... 그럭저럭... ;;;;;
아래 문제와 같이
분자가 일차식인 분수식의 적분은 풀이가 2개 있습니다.

일단, 식부터 변형

로 놓고
a, b값을 구하면

그런데, 이걸 이렇게 힘들게(?) 적분 안 하죠
분모를 미분해서 분자를 만들 수 있으니까 바로 적분합니다.
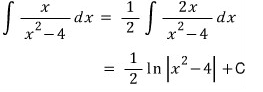
잠깐 옆으로 샐께요
위에서 바로 적분한다고 표현했지만
사실은 치환적분입니다.

그런데, 우리는
치환따위(?) 하지 않아도 바로 적분할 수 있으니까
그냥 바로 적분한 것 뿐입니다. ;;;;;
암튼, 다시 돌아와서
이렇게 분모를 미분해서 분자를 만들 수 있는 경우에는
분수식을 변형해서 적분하든, 바로 적분하든 상관없지만 (물론, 바로 적분하겠죠..?!)
아래 문제와 같이
분모를 미분해서 분자를 만들 수 없는 경우에는
분수식을 변형해서 적분하는 수 밖에 없습니다.
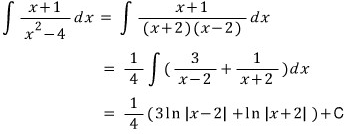
(처음에 말했듯이
분수식의 변형은 '분수식의 변형 (1), (2), (3)'을 참고하세요~)
잔머리 굴려서
이렇게 푸는 학생들도 있는데
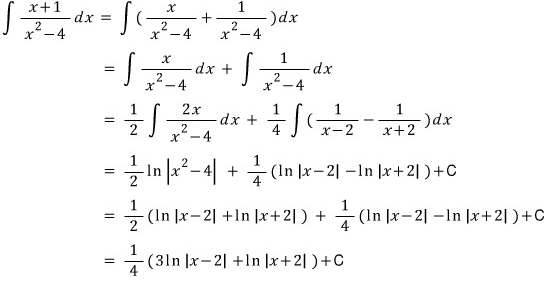
연습하려고 일부러 이렇게 어렵게 푸는 게 아니라면
제발 이러지 마세요~ ;;;;;
하나 더 해볼께요
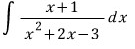
이 문제는
분모를 미분해서 분자를 만들 수 있으므로
위에서 말한 풀이가 모두 가능합니다.
분수식을 변형해서 적분
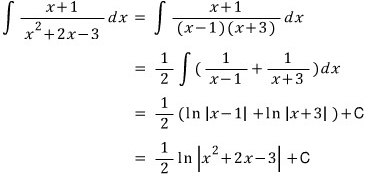
바로 적분
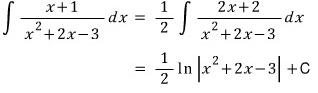
치환해서 적분
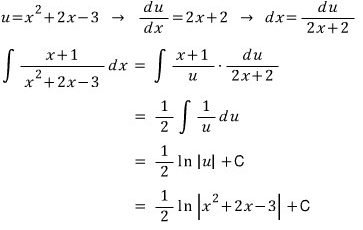
하지만
상수항만 살짝 바뀐 이 분수식은
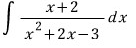
분모를 미분해서 분자를 만들 수 없으므로
분수식을 변형해서 적분하는 수 밖에 없습니다.
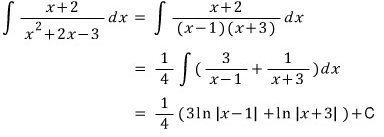
③ 분모가 인수분해 안 되는 이차식인 경우
분모가 인수분해 되지 않더라도
분모를 미분해서 분자를 만들 수 있으면
위에서 푼 것과 똑같이 풀면 됩니다.
다만, 분모가 인수분해 되지 않으니까
분수식을 변형하는 건 안 되고
바로 적분하거나
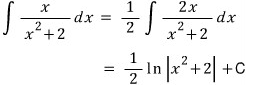
치환해서 적분하거나
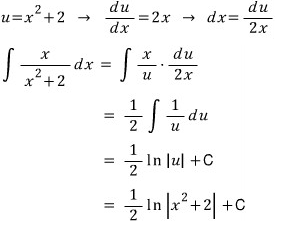
문제는
분모가 인수분해도 되지 않으면서
분모를 미분해서 분자를 만들 수도 없는 경우입니다.
이런 경우는 적분이 어렵기 때문에
문제로 나오는 유형은 딱 한가지입니다.
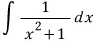
이런 적분은 치환으로 문제를 풉니다.
그것도 아주 이상한(?) 치환..!!
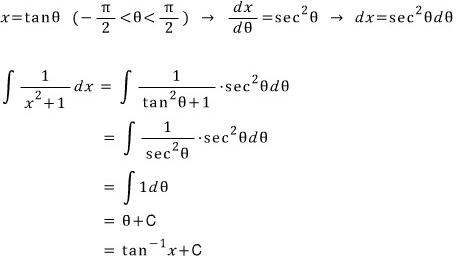
참고로
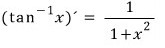
그냥 그렇다구요... 신경쓰지 마세요~ ;;;;;
다행히도(?) 탄젠트의 역함수는 고교과정에 나오지 않기 때문에
이런 문제는 정적분으로만 출제됩니다.

나름 분수식의 적분을 분류해 봤는데
빠진 유형이 있는지 모를겠네요... 없기를... ^-^//
요기로 가면 → www.gajok.co.kr/math.html
다른 글들도 편리하게 볼 수 있습니다.

'수학' 카테고리의 다른 글
| 구분구적법 (2) (0) | 2022.03.16 |
|---|---|
| 구분구적법 (1) (2) | 2022.03.08 |
| 접선의 방정식 (4) (0) | 2022.02.10 |
| 접선의 방정식 (3) (0) | 2022.02.04 |
| 미분계수 (4) (0) | 2022.01.25 |